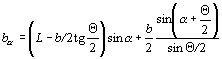СП 32-102-95 Сооружения мостовых переходов и подтопляемых насыпей. Методы расчета местных размывов
СИСТЕМА НОРМАТИВНЫХ
ДОКУМЕНТОВ
В СТРОИТЕЛЬСТВЕ
СВОД ПРАВИЛ
СООРУЖЕНИЯ
МОСТОВЫХ ПЕРЕХОДОВ
И ПОДТОПЛЯЕМЫХ НАСЫПЕЙ
МЕТОДЫ РАСЧЕТА
МЕСТНЫХ РАЗМЫВОВ
СП 32-102-95
КОРПОРАЦИЯ «ТРАНССТРОЙ»
МОСКВА
1996
Предисловие
1. Разработан Научно-исследовательским институтом транспортного строительства (АО «ЦНИИС»).
Внесен Корпорацией «Трансстрой».
2. Согласован Федеральным дорожным департаментом Минтранспорта РФ (№ АТО-8/150 от 11.11.94) и ЦНИ МПС (№ ЦПИ-4/16 от 20.12.94).
3. Одобрен Минстроем РФ (№ 13-238 от 05.06.95).
Принят и введен в действие Корпорацией «Трансстрой» (№ МО-298 от 22.12.95).
5. Взамен ВСН 62-69 «Технические указания по расчету местного размыва у опор мостов, струенаправляющих дамб и траверсов».
Введение
Главное задачей настоящего свода правил является упорядочение как принципиальных подходов, так и методов расчета местных размывов в зависимости от типа сооружений и их взаимодействия с потоком.
Свод правил разработан АО «ЦНИИС» (ответственный исполнитель - канд. техн. наук В.Ш. Цыпин) на основе накопленных в России и за рубежом за несколько десятилетий данных о местных размывах, по результатам лабораторных гидравлических исследований, натурных наблюдений на естественных водотоках и на эксплуатируемых мостовых переходах, а также с учетом опыта проектирования и строительства мостовых переходов.
Приведенные правила и положения позволяют по сравнению с имеющимися зарубежными аналогами более полно учесть в расчетах реальные условия работы сооружений и повысить достоверность определения глубин воронок местных размывов.
СП 32-102-95
СВОД ПРАВИЛ
СООРУЖЕНИЯ МОСТОВЫХ ПЕРЕХОДОВ И ПОДТОПЛЯЕМЫХ НАСЫПЕЙ
МЕТОДЫ РАСЧЕТА МЕСТНЫХ РАЗМЫВОВ
CONSTRUCTIONS OF BRIDGES AND ABUTMENTS
METHODS OF LOCAL SCOUR CALCULATION
Дата введения 1996-04-01
1 Область применения
Настоящий свод правил устанавливает методы расчета глубин местных размывов у оснований сооружений железных и автомобильных дорог при воздействии на них водного потока и волн.
Положения настоящего документа обязательны для предприятий, организаций и объединений независимо от их форм собственности и принадлежности, осуществляющих проектирование, строительство и эксплуатацию сооружений на железных и автомобильных дорогах.
2 Нормативные ссылки
В настоящем своде правил использованы ссылки на следующие документы:
СНиП 2.02.01-83* Основания зданий и сооружений.
СНиП 2.05.03-84* Мосты и трубы.
СНиП 2.06.04-82* Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов).
ГОСТ 20522-75 Грунты. Метод статистической обработки результатов определения характеристик.
3 Определения
В настоящем своде правил применены термины в соответствии со СНиП 2.06.04-82*, СНиП 2.02.01-83* и СНиП 2.05.03-84*.
4 Общие положения
4.1 Расчет местного размыва производится для следующих сооружений мостовых переходов:
- промежуточных опор мостов;
- береговых опор мостов, грани которых выступают из конуса;
- насыпей пойменных подходов и в долинах рек, в том числе на прижимных участках, когда часть откоса насыпи попадает в русло;
- струенаправляющих дамб и конусов мостов, регулирующих пойменный поток;
- сплошных незатопляемых поперечных регуляционных сооружений, отжимающих поток от пойменных насыпей (траверсы) или от берегов и насыпей на прижимных участках рек (буны, шпоры и т.п.), а также затопляемых сооружений (типа полузапруд).
4.2 Глубину местного размыва следует определять для условий возможных наиневыгоднейших положений русла и наносных скоплений, выявляемых с учетом руслового процесса в районе перехода:
- у промежуточных и береговых опор - после окончания общего размыва подмостового сечения;
- у струенаправляющих дамб - на пике расчетного паводка;
Если расчет общего размыва производится по допускаемым скоростям течений, то с некоторым завышением местные размывы допускается определять на момент 50 % полного размыва при продолжительных паводках (к которым следует относить снеговой сток) и 25 % размыва при непродолжительных (ливневых);
- у других сооружений, расположенных на пойме, - на пике расчетного паводка;
- у других сооружений, расположенных в русле, за расчетный принимают наибольший размыв, определенный при расчетном уровне и уровне, соответствующем протеканию потока в бровках русла.
Если в расчетах глубина размыва получается отрицательной, то глубину размыва принимают равной нулю (размыв отсутствует).
4.3 Расчетную (наинизшую) отметку у основания сооружений после местного размыва следует определять, отсчитывая полученную согласно настоящим нормам глубину местного размыва:
- у опор - от расчетной отметки дна на соответствующей вертикали после общего размыва (с учетом возможного перемещения в русле вертикали с наибольшей глубиной потока);
- у прочих сооружений - от бытового дна с учетом естественного переформирования русла или возможных изменений в гидрографической сети в районе перехода.
4.4 Расчет местного размыва предусматривается в двух случаях:
а) когда в воронку размыва беспрепятственно поступают наносы, влекомые потоком;
б) когда поток не влечет наносов или какая-либо причина исключает их поступление в воронку размыва.
К последнему случаю относятся водотоки и их участки, на которых скорость при расчетном паводке менее размывающей для грунтов русла, а также пойменные потоки на задернованных и заросших поймах. К этому же случаю относятся условия, когда русловые деформации в подмостовом сечении протекают при дефиците донных наносов (например, при волне попуска).
4.5 Для определения глубины местного размыва необходимы следующие данные: гидравлические характеристики бытового и стесненного потоков у сооружений и в отверстии моста; характеристики грунтов в пределах ожидаемого местного размыва; очертания и размеры сооружений; их положение относительно направления потока. Исходные данные получают в результате топографических, гидрометрических и геологических работ, выполненных на стадии изысканий, а также на основе лабораторных анализов и в процессе проектирования.
4.6 При определении расчетных характеристик грунтов, а также их связности и неоднородности необходимо пользоваться приложением А.
4.7 При надлежащем обосновании в проектах могут быть использованы коррективы или методы определения местных размывов, не включенные в нормы.
5 Промежуточные опоры мостов
5.1 Размыв в однородных несвязных грунтах
5.1.1 В расчетах грунт следует считать однородным, если местный размыв происходит за счет выноса из воронки размыва всех входящих в несвязный материал разнозернистых частиц. Требования, обеспечивающие указанное условие, изложены в приложении А (п. А.4).
5.1.2 Наибольшую глубину местного размыва h, м, в однородном несвязном грунте у опоры (в виде одиночно стоящей сваи, сваи-оболочки и т.п.), имеющей от уровня воды до дна воронки местного размыва постоянную ширину поперечного сечения (рисунок 5.1), следует определять по формулам:
- при поступлении наносов в воронку размыва (υ ³ υ0)
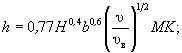 (5.1)
(5.1)
- без поступления наносов в воронку размыва
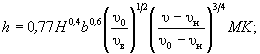 (5.2)
(5.2)
где b - расчетная ширина (поперечное сечение) опоры, равная ширине ее передней грани, м;
υ, H - средняя скорость, м/с, и глубина потока, м, перед опорой после общего размыва;
υ 0 , υв - размывающая и взмучивающая скорости потока для грунта, в котором происходит местный размыв, м/с, (см. приложение А и п. 5.1.5);
υн - начальная скорость, м/с, (см. п. 5.1.6);
M , K - коэффициенты формы (см. п. 5.1.9) и косины (см. п. 5.1.10) опоры.
5.1.3. Наибольшую глубину местного размыва, м, в однородном несвязном грунте у опоры на массивном фундаменте, имеющей от уровня воды до дна воронки местного размыва переменную ширину поперечного сечения (рисунок 5.2), следует определять по формулам:
- в случае, предусмотренном п. 4.4.а,
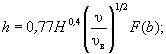 (5.3)
(5.3)
- в случае, предусмотренном п. 4.4.б,
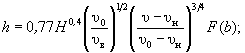 (5.4)
(5.4)
где F(b) - параметр, учитывающий геометрию опоры, м0,6; определяется по формуле
![]() (5.5)
(5.5)
где bi - ширина поперечного сечения i-го из n имеющихся выше отметки дна после общего размыва элементов опоры с постоянной шириной, м (рисунок 5.3);
Мi , Ki - коэффициенты формы и косины i-го элемента опоры, определяемые соответственно по пп. 5.1.9 и 5.1.10;
fi - весовой коэффициент, приходящийся на i-й элемент опоры (см. п. 5.1.8).
5.1.4. Наибольшую глубину местного размыва в однородном несвязном грунте у опор на свайном основании следует определять в зависимости от положения низа плиты ростверка е относительно дна русла после общего размыва (рисунок 5.4 ):
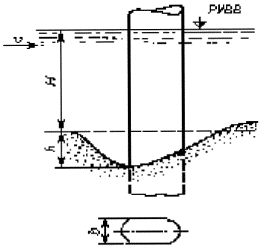
Рисунок 5.1 - Опора с постоянной шириной от расчетного уровня воды (РУВВ) до дна воронки местного размыва
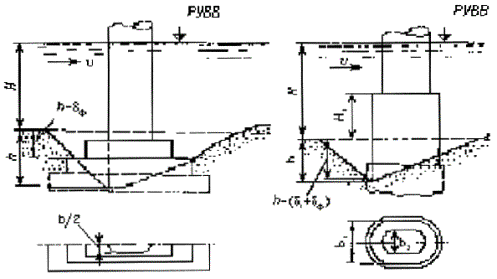
Рисунок 5.2 - Схемы опор на массивном фундаменте:
а - с постоянной шириной в пределах глубины потока; б - с переменной шириной в пределах глубины потока
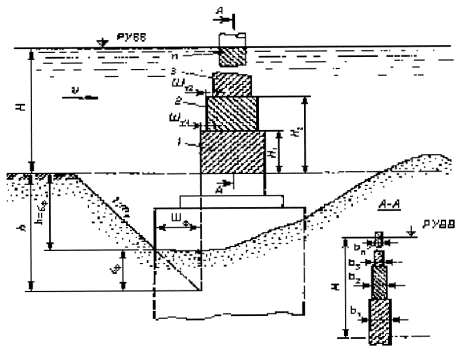
Рисунок 5.3 - Разделение опоры на элементы (1, 2, 3, ... n) с постоянной шириной
а) при e ³ 0,3H по формулам ( 5.3) или ( 5.4) в зависимости от режима наносов;
б) при е < 0,3Н по формуле
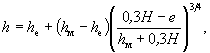 (5.6)
(5.6)
где hе - глубина размыва, определяемая по формулам ( 5.3) или ( 5.4) при положении низа плиты ростверка относительно дна после общего размыва, равном е = 0,3Н (рисунок 5.5);
h м - то же, при плите ростверка, низ которой заглублен ниже отметки возможных размывов (а ее верх - на проектной заданной отметке).
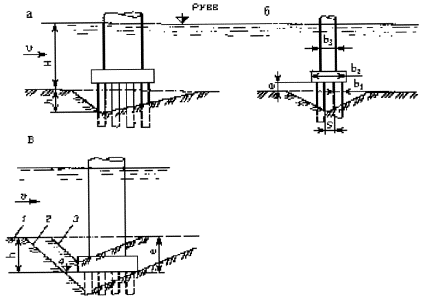
Рисунок 5.4 - Схема опор на свайном фундаменте:
а и б - профиль и фасад опоры с плитой ростверка выше дна русла после общего размыва; в - профиль опоры с плитой ростверка ниже дна русла:
1 - дно русла; 2 - сечение воронки размыва при расчете как для опоры на массивном фундаменте (т.е. без учета свайного основания); 3 - то же, с учетом свайного основания; 4 - расчетная отметка дна воронки размыва, когда глубина размыва, определенная без учета свайного основания, больше глубины заделки низа плиты ростверка е и меньше е при учете свайного основания
Если глубина размыва, определенная по формуле ( 5.6), окажется меньше глубины заделки низа плиты ростверка в русло от отметки общего размыва (h < |e |), то расчет местного размыва следует производить по формулам ( 5.3) или ( 5.4) как для опор на массивном фундаменте. Если при этом отметка дна воронки окажется ниже подошвы плиты ростверка, то в расчете следует принимать глубину размыва до отметки подошвы плиты ростверка (см. рисунок 5.4.в).
5.1.5. Взмучивающую скорость υ в , м/с, характеризующую мутность потока (т.е. содержание взвешенных наносов в единице объема воды) определяют по формуле
![]() (5.7)
(5.7)
где g - ускорение свободного падения (g = 9,8 м/с2);
ω - гидравлическая крупность размываемого грунта, м/с; принимается по приложению А (табл. А.4).
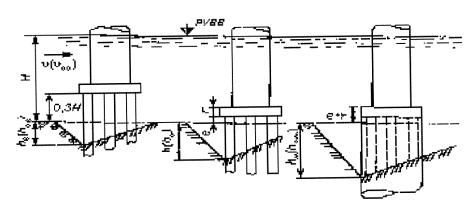
Рисунок 5.5 - Промежуточные и исходные глубины размыва у опор на свайном фундаменте при е < 0,3Н (в скобках даны характеристики, определяемые при расчете размывов в неоднородных несвязных грунтах):
а - низ ростверка расположен на высоте 0,3Н над дном русла после общего размыва; б - проектное положение плиты ростверка; в - низ плиты ростверка заглублен ниже отметки возможных местных размывов (а ее верх - на проектной заданной отметке)
5.1.6 Минимальная скорость набегающего потока, при которой частицы грунта у опоры приходят в движение и появляются первые признаки размыва, называется начальной скоростью υн, м/с, которую определяют по формуле
![]() (5.8)
(5.8)
где ![]()
b - расчетная ширина опоры, м (см. п. 5.1.7);
d - средний диаметр частиц грунта, м (см. п. А.3).
Если по формуле ( 5.8) получается υ н ³ 0,9 υ 0 , то следует принимать υ н = 0,9 υ 0 .
5.1.7 Расчетную ширину опоры b, м, с n элементами выше отметки общего размыва следует определять по формуле
![]() (5.9)
(5.9)
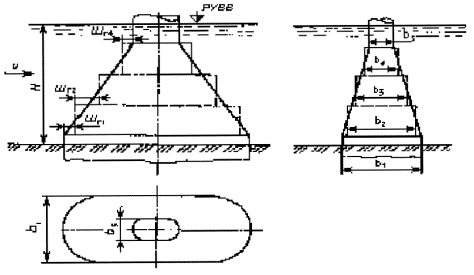
Рисунок 5.6 - Разделение на элементы тела опоры при недискретном изменении ее размеров
При определении расчетной ширины опоры на свайном фундаменте по формуле ( 5.9) в качестве расчетной ширины свайного фундамента необходимо принимать ширину одной сваи.
У опор на участке с недискретным (плавным) изменением ширины поперечного сечения следует выделять не менее трех одинаковых по высоте элементов, для которых в качестве расчетной ширины поперечного сечения bi принимают среднюю ширину рассматриваемых элементов (рисунок 5.6).
5.1.8 Весовой коэффициент i-го элемента опоры (см. рисунок 5.3 ) следует определять по формуле
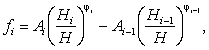 (5.10)
(5.10)
где А, j - коэффициент и показатель степени, принимаемые в зависимости от относительной высоты до верха Нi / Н i-го и Нi-1 / Н (i - 1)-го элементов:
при Hi / H ³ 0,3 (или Hi-1 / H ³ 0,3) A = 1, j = 1/3;
при Hi / H < 0,3 (или Hi-1 / H < 0,3) A = 2,23, j = 1.
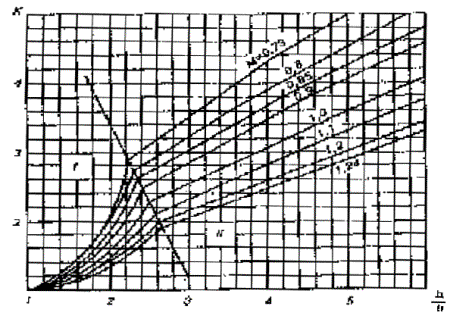
Рисунок 5.7 - График для определения коэффициента косины K
Для последнего (находящегося у поверхности потока) n-го элемента Нn = Н.
Весовые коэффициенты первого и последнего элементов опоры соответственно равны
f 1 = A1(H1 / H) j 1 , (5.11)
fn = 1 - An-1(Hn-1 / H) j n -1 . (5.12)
5.1.9. Коэффициент формы опоры М или элемента опоры Мi должен приниматься следующим:
Форма опоры Коэффициент М
Цилиндрическая ............................................................................ 1,0
С овальной или полуциркульной передней гранью .................. 0,85
Прямоугольная .............................................................................. 1,24
С верховой стороны в виде двугранного угла Q :
120 ° ................................................................................................. 1,22
90 ° .................................................................................................... 1,0
60 ° ................................................................................................... 0,73
Для прямоугольной опоры с закругленными углами коэффициент формы следует определять в зависимости от отношения радиуса закругления r и ширины опоры b:
2r / b 0 0,2 0,4 0,5 0,6 0,7 0,8 0,9 1
М 1,24 1,20 1,18 1,15 1,11 1,07 1,01 0,94 0,85
Формы рассматриваемых опор приведены в справочном приложении В.
Коэффициент формы при двугранном угле Q с верховой стороны опоры в пределах 30 ° £ Q £ 120 ° допускается определять по формуле
М = ( Q /90 ° )3/4.
Коэффициент формы свайного фундамента следует определять по приложению Б.
5.1.10 Если продольная ось опоры образует с направлением набегающего на нее потока угол a > 1 0 ° , глубины размыва h следует определять с учетом коэффициента косины K . Коэффициент косины для всей опоры K или элемента опоры K i определяют по графику (рисунок 5.7 ) или по формулам
при b a / b £ 2,53 M 1/3 (зона I)
![]() (5.13)
(5.13)
при b a / b > 2,53 M 1/3 (зона II)
![]() (5.14)
(5.14)
где b a - приведенная ширина опоры или ее элемента, равная ширине их проекции на плоскость, нормальную направлению потока, м.
Расчетные формулы для определения приведенных ширин характерных форм опор даны в приложении В.
Косина набегания потока на свайное основание опор (на ряд опор, расположенных по фасаду к направлению течения) учитывается только коэффициентом косины у отдельно стоящей сваи.
Примеры расчета глубин местного размыва у промежуточных опор приведены в приложении Г.
5.1.11 Ступени, образующиеся в теле опоры и массивном фундаменте переменного сечения, приводят к снижению глубины размыва, которое может быть определено по приложениям Д и Е.
Уменьшение глубины размыва d т за счет ступеней на границе элементов промежуточной опоры, находящихся выше отметки общего размыва, рекомендуется учитывать по приложению Д при расположении ступеней на глубине потока ниже 0,5Н и имеющих суммарную ширину больше половины ширины элемента опоры, находящегося выше верхней ступени (см. рисунки 5.2 и 5.3).
Уменьшение глубины размыва d ф за счет обнажаемой в процессе местного размыва части массивного фундамента рекомендуется учитывать по приложению Е, когда суммарная ширина обнажаемых ступеней фундамента составляет не менее 15 - 20 % от ширины грани опоры (или фундамента), располагающейся непосредственно выше отметки общего размыва.
В случаях, когда указанные выше условия не удовлетворяются, уменьшение глубин размыва d т и d ф незначительно и его можно не учитывать.
5.1.12 При резком изменении гидравлических характеристик потока под мостом (интенсивные ливневые паводки, волны попуска в нижнем бьефе плотин, аварийные сбросы воды из водохранилищ и т.п.) допускается определять глубину местного размыва с учетом времени воздействия потока на размываемое у основания опоры.
Учет фактора времени эффективен при отношении расчетной ширины опоры b (см. п. 5.1.7) к времени Т воздействия потока b / T > 2 ¸ 3 м/сут.
5.2 Учет неоднородности несвязных грунтов
5.2.1 Несвязный грунт является неоднородным, т.е. образует естественную отмостку в воронке местного размыва, если удовлетворяются требования, изложенные в п. А.5.
5.2.2 Наибольшую глубину местного размыва в неоднородном по крупности несвязном грунте h, м, определяют по формулам:
а) при e υ > υ нD
для опор на свайном основании при e < 0,3H (см. рисунок 5.4)
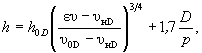 (5.15)
(5.15)
для всех остальных типов фундаментов
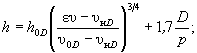 (5.16)
(5.16)
б) при e υ £ υ нD
![]() (5.17)
(5.17)
где e - коэффициент абразивности (см. п. 5.2.3);
υ нD , υ 0D - начальная (см. п. 5.1.6) и размывающая (см. п. А.6) средние скорости потока, м/с, для среднего диаметра частиц D слоя отмостки, м, которых содержится в грунте (по массе) p долей (см. п. 5.2.4);
h cD - глубина местного размыва в однородном несвязном грунте со средним диаметром частиц D при скорости потока υ = υ 0D у опор на свайном фундаменте, когда е < 0,3Н (см. п. 5.1.4), определяемая по формуле
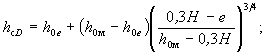 (5.18)
(5.18)
h 0e , h0m - глубина местного размыва в однородном несвязном грунте со средним диаметром частиц D и при скорости потока υ = υ 0D соответственно при положении низа плиты ростверка относительно дна после общего размыва е = 0,3Н и при плите ростверка, низ которой заглублен ниже отметки возможных местных размывов (см. рисунок 5.5);
h 0D - то же для опор на массивном фундаменте и свайном основании при e ³ 0,3H.
Глубина размыва h0e, h0м и h0D определяют по формуле
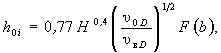 (5.19)
(5.19)
где υ вD - взмучивающая скорость потока для грунта со средним диаметром частиц D (см. п. 5.1.5).
5.2.3 Коэффициент абразивности e характеризует уменьшение устойчивости крупных частиц в потоке, находящихся среди более мелких и подвижных фракций. При размыве несвязных грунтов значения коэффициента e следует принимать равным:
D /dм £ 3 4 6 8
e 1 1,19 1,16 1,14
D /dм 10 12 15 20 30
e 1,125 1,11 1,09 1,075 1,06
или по формуле при D / dм > 3
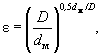 (5.20)
(5.20)
где dм - средний диаметр частиц мелких фракций, который определяют по формуле
![]() (5.21)
(5.21)
При D / dм > 30 можно принимать e = 1.
В случае, предусмотренном п. 4.4.а, когда известен средний диаметр частиц наносов, поступающих в воронку местного размыва, последний следует принимать за расчетное значение dм.
5.2.4 Средний диаметр частиц слоя отмостки D, м, и их содержание в грунте (по массе) р следует определять:
а) при ![]() - подбором из уравнения
- подбором из уравнения
p / D = Rp, (5.22)
где 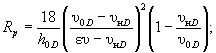 (5.23)
(5.23)
![]() - коэффициент
абразивности и начальная скорость для самых крупных частиц (или включений) в
грунте со средним диаметром частиц Dmax
(см. п. А.4).
- коэффициент
абразивности и начальная скорость для самых крупных частиц (или включений) в
грунте со средним диаметром частиц Dmax
(см. п. А.4).
Если определяют глубину размыва у опоры на свайном основании при е < 0,3Н, то в формуле ( 5.23) вместо h0D следует принимать глубину размыва hcD по формуле ( 5.18).
Порядок определения среднего диаметра частиц слоя отмостки D и их содержание в грунте р из уравнения ( 5.22), а также пример расчета глубины местного размыва в неоднородном несвязном грунте изложен в приложении Ж;
б)
при ![]() - по формуле
- по формуле
![]() ( 5.24)
( 5.24)
где Dmin - минимальная крупность частиц в слое отмостки.
Определение Dmin, м, следует начинать с расчета по формуле
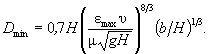 (5.25)
(5.25)
При наличии в грунте частиц крупнее полученного значения менее 15 % размер частиц принимают за искомый, а более или равное 15 % - размер частиц, полученных по формуле ( 5.25), умножают на коэффициент 0,5. Если частиц полученной крупности Dmin грунт не содержит, то искомыми частицами Dmin будут ближайшие к рассчитанным более крупные частицы;
в) при наличии в грунте крупных включений (см. п. А.5) не менее 2 % - значение D принимают равным среднему диаметру частиц этих включений.
5.3 Размыв в связных грунтах
5.3.1 К связным относятся глинистые, суглинистые и супесчаные грунты с числом пластичности Wп ³ 0,01 (см. п. А.7).
При расчете местных размывов к связным также относятся:
а) глинистые, суглинистые, супесчаные и песчаные грунты при заторфованности (содержании растительных остатков) более 10 %;
б) пылеватые пески, содержащие более 20 % по массе пылеватых частиц (мельче 0,10 мм).
5.3.2 Наибольшую глубину местного размыва в связном грунте h, м, следует определять по формуле (для всех фундаментов опор, кроме свайного при e < 0,3H)
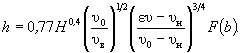 (5.26)
(5.26)
Глубину размыва у опоры на свайном основании при е < 0,3Н следует определять по формуле ( 5.6), в которой глубины размыва h e и hм находят по формуле ( 5.26).
При определении наибольшей глубины размыва по формуле ( 5.26) необходимо принимать:
- коэффициент абразивности e = 1,16 при поступлении в воронку размыва песчаных наносов и e = 1, когда нет поступления наносов;
- в формуле начальной скорости υ н в качестве среднего диаметра частиц грунта - утроенную толщину отрывающихся отдельностей, т.е. d = 3z, где z - толщина отрывающихся отдельностей, мм,
z = 0,35 + 0,6cp10 - 4 . (5.27)
Здесь ср - расчетное сцепление, Па.
Пример расчета размывов в связных грунтах приведен в приложении Г.
5.3.3. В случае, предусмотренном в п. 4.4 .а, когда поток влечет наносы, за расчетную глубину в неоднородных несвязных и связных грунтах следует принимать меньшую из глубин, полученных по формулам соответственно ( 5.15 ) - ( 5.17 ) или ( 5.26 ) и по формуле ( 5.3 ) или ( 5.6 ) в зависимости от типа фундамента опор для грунта, влекомого потоком.
В случае, предусмотренном в п. 4.4.б, за расчетную глубину в неоднородных несвязных грунтах принимают меньшую из глубин, полученных по формулам ( 5.15) - ( 5.17) или ( 5.26) и по формулам ( 5.4) или ( 5.6) для грунта, средний диаметр частиц которого dм определяют по формуле ( 5.21).
5.4 Учет слоистого залегания грунтов
5.4.1 Залегание грунтов следует считать слоистым, если:
а) в процессе местного размыва вскрывается грунт, по физико-механическим свойствам (крупности или нормативному удельному сцеплению) отличающийся от вышележащего;
б) в процессе общего размыва вскрывается грунт, по физико-механическим свойствам отличающийся от грунта, влекомого потоком.
В последнем случае в расчетах толщину слоя влекомых наносов следует принимать равной нулю.
5.4.2 Расчет местного размыва у опор мостов при слоистом залегании грунтов ведут в соответствии с требованиями, изложенными в обязательном приложен ии И. При этом необходимо учитывать следующее:
а) когда вышележащий слой подстилает более размываемый грунт, должно быть обеспечено условие, при котором рассчитанная глубина размыва в верхнем слое грунта h, м, не должна доходить до нижней границы этого слоя на величину
D d > 0,15h . (5.28)
В противном случае расчет размыва производят по параметрам нижнего более размываемого слоя;
б) если при расчете одного из нижних слоев глубина размыва окажется меньше суммы вышележащих слоев å D , то следует принимать, что размыв прекратится на поверхности рассматриваемого слоя.
Пример расчета размывов в слоистых грунтах приведен в приложении И.
6 Струенаправляющие дамбы и конуса мостов
6.1 Размыв в однородных несвязных и связных грунтах*
* Неоднородность и связность грунтов определяют так же, как при расчете промежуточных опор.
6.1.1 Наибольшую глубину местного размыва h, м, в однородных несвязных и связных грунтах у голов струенаправляющих дамб и в верховой части конусов мостов следует определять по формуле
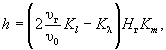 (6.1)
(6.1)
где υ г , Hг - скорость, м/с (см. п. 6.1.2) и глубина потока, м (см. п. 6.1.4) у подошвы головы дамбы или конуса;
υ 0 - размывающая скорость для грунтов, в которых происходит размыв, м/с (см. п. А.8);
Kl - коэффициент, характеризующий увеличение скорости потока в голове дамбы или в верховой части конуса при недостаточной длине сооружения; определяется по приложению К.
K l - коэффициент, принимаемый равным 1,0, когда дамба или конус обтекаются потоком, и 0,85 при плохо обтекаемых сооружениях;
Km - коэффициент, зависящий от коэффициента заложения откоса или конуса дамбы m со стороны русла:
m ................. 1,0 1,5 2,0 2,5 3,0
K m ................. 1 0,94 0,80 0,70 0,67
Если при расчете по формуле ( 6.1) глубина размыва получается меньше нуля, то глубину размыва принимают равной нулю.
Пример расчета местных размывов у дамб и конусов моста приведен в приложении Л.
6.1.2 Скорость потока в голове дамбы или в верховой части конуса υ г , м/с, следует определять в зависимости от числа пойм, на которых устраивают струенаправляющие дамбы, по формулам:
а) при односторонней пойме
![]() (6.2)
(6.2)
б) при пересечении водотока с двумя поймами со стороны мощной (пропускающей больший расход воды) υ г(м) и слабой υ г(с) пойм соответственно:
![]() (6.3)
(6.3)
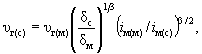 (6.4)
(6.4)
где Сг, Сгм - коэффициент Шези, м0,5/с, определяется по коэффициенту шероховатости русла nр при глубине потока на односторонней Hг и на мощной Hгм, м (см. п. 6.1.4) поймах по формуле
![]() или
или ![]() (6.5)
(6.5)
d (или d м , d с ) - коэффициент стеснения потока подходами на одной пойме Qп / Q или со стороны соответственно мощной Qпм / Q и слабой Qпс / Q пойм;
Q пi - расход воды в расчетный паводок, проходящий в бытовом состоянии на части i-й поймы, перекрытой насыпью;
Q - расчетный расход воды в речной долине;
i - продольный уклон свободной поверхности нестесненного потока в расчетный паводок;
i м - средний уклон свободной поверхности потока перед мостом (см. п. 6.1.3);
i м(м) , iм(с) - фиктивные средние уклоны свободной поверхности потока перед мостом со стороны соответственно мощной и слабой пойм (см. п. 6.1.3);
b - показатель степени, определяемый по формуле
![]() (6.6)
(6.6)
Если правая часть формулы ( 6.6) получается меньше 0,2, то следует принимать b = 0,2.
Уклоны в формулах ( 6.2) - ( 6.4) принимают в долях единицы.
При расчете местных размывов у струенаправляющих дамб и верховой части конусов моста участок реки следует рассматривать как с одной поймой, если по другой проходит менее 5 % расчетного расхода.
6.1.3 Средний уклон свободной поверхности потока перед мостом следует определять по формулам:
- при пересечении водотока с одной поймой
![]() (6.7)
(6.7)
- при пересечении водотока с двумя поймами
![]() (6.8)
(6.8)
где Х0 - расстояние от моста до вертикали, где устанавливается предмостовой подпор D h в ;
j - коэффициент, характеризующий долю предмостового подпора, вызванную стеснением i-й поймы (мощной - с индексом «м», слабой - с индексом «с»), определяется по формуле:
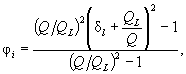 (6.9)
(6.9)
QL - расход воды, проходящий при отсутствии стеснения на ширине отверстия моста.
При косом пересечении поймы подходом, если расстояние вверх по течению от створа моста до выхода насыпи за пределы размыва S0в > X0, то в формуле ( 6.8) принимают Х0 = S0в.
6.1.4 Глубину потока Hгi, м, у подошвы головы дамбы со стороны i-й поймы можно принимать равной:
H ri = H б i + D h в , (6.10)
где Hбi - глубина потока на вертикали у подошвы головы дамбы в бытовых условиях (до устройства мостового перехода) со стороны i-й поймы, м.
6.2 Учет неоднородности и слоистого залегания грунтов
6.2.1 Наибольшую глубину местного размыва в неоднородных по крупности несвязных грунтах у голов струенаправляющих дамб и в верховой части конусов моста следует определять по формулам:
а) при υ г > 0,5 υ 0D K l / Kl
h = hD + 1,3D / p, (6.11)
б ) при υ г £ 0,5υ0DK l / Kl
h = 1,3D / p, (6.12)
где hD - глубина размыва, определяемая по формуле ( 6.1), в которой вместо υ 0 принимают υ 0D - размывающую скорость для среднего диаметра частиц D в слое отмостки (см. п. 6.2.2).
К расчету следует принимать меньшую из глубин, получаемых по формулам ( 6.11) или ( 6.12) и по формуле ( 6.1) для грунта, средний диаметр частиц которого dм определяют по формуле ( 5.21).
6.2.2 Средний диаметр частиц слоя отмостки D, м, и их содержание в грунте по (массе) р следует определять:
а) в случае, предусмотренном п. 6.2.а, - подбором из уравнения:
![]() (6.13)
(6.13)
При решении уравнения и назначении расчетных значений D и р поступают, как при расчете размывов у опор в аналогичных условиях по приложению Ж;
б) в случае, предусмотренном п. 6.2.б, - по гранулометрическому составу грунта согласно п. 5.2.4.б. При этом определение минимальной крупности частиц Dmin, м, входящих в слой отмостки, следует начинать с расчета по формуле
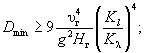 (6.14)
(6.14)
в) при наличии в грунте крупных включений (см. приложение А) - по среднему диаметру частиц этих включений.
6.2.3 В случаях, когда пойма в районе расположения струенаправляющей дамбы сложена слоями различных грунтов, при определении глубин размывов следует пользоваться рекомендациями п. 5.4.2 и приложения И применительно к дамбам:
а) при однородных по крупности несвязных грунтах в слоях с залеганием сверху более мелкого грунта, а также при верхнем более мелком неоднородном по крупности грунте - по формуле ( 6.1) для обнажаемого грунта;
б) при нижнем
связном материале, размывающая скорость которого больше, чем вышележащего
несвязного грунта (однородного или неоднородного), - по формуле ( 6.1)
для обнажаемого связного материала с учетом абразивного воздействия на него
несвязных частиц (для чего первый член в скобках принимают равным ![]() , где e = 1,16).
, где e = 1,16).
в) при однородных и неоднородных по крупности слоях с залеганием слоя из мелкого грунта (со средним диаметром частиц d2) ниже крупного (со средним диаметром частиц d1), а также при нижнем связном материале, размывающая скорость которого меньше, чем вышележащего грунта - по формуле
h = h2 - h d , (6.15)
где h d - снижение размыва из-за заноса воронки более крупным грунтом верхнего слоя, определяемое по формуле
![]() (6.16)
(6.16)
h 2 , h1 - глубина местного размыва, определяемая по формуле ( 6.1) для соответственно нижнего и верхнего слоев грунта (неоднородность грунтов не учитывается);
D - толщина верхнего слоя грунта.
г) при расположении в нижнем слое крупного неоднородного по составу несвязного грунта в случае, предусмотренном п. 6.2.1.а и при hD ³ D - по формуле ( 6.11); в остальных случаях по формуле
h = D + 1,3D / p. (6.17)
7 Поперечные регуляционные сооружения и береговые опоры
7.1 У сплошных затопляемых поперечных сооружений и береговых опор, боковая грань которых не обсыпана конусом, при коэффициенте стеснения потока d £ 0,15 (см. п. 6.1.2 ) наибольшую глубину местного размыва в однородных несвязных и связных грунтах следует определять по формулам:
- при ![]()
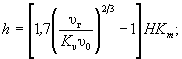 (7.1)
(7.1)
- при ![]()
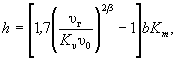 (7.2)
(7.2)
где b - расчетная ширина сооружения, м (см. приложение М);
υ г - скорость потока в голове поперечного сооружения или у боковой грани береговой опоры, м/с (см. п. 7.3);
K υ - коэффициент, характеризующий поступление наносов в воронку размыва и определяемый по приложению Н;
Н - глубина потока в голове поперечного сооружения или у боковой грани береговой опоры в расчетных условиях, м (с учетом естественного руслового процесса и общего размыва);
υ 0 - размывающая скорость, м/с, определяемая с учетом глубины потока Н;
K m - коэффициент, зависящий от коэффициента заложения откоса m рассматриваемых сооружений, определяемый согласно п. 6.1.1.
За расчетную глубину размыва в связном грунте, когда поток влечет несвязные наносы, следует принимать меньшее из значений, получаемое по формулам ( 7.1) или ( 7.2) для связного грунта и грунта, влекомого потоком.
Примеры расчета по формулам ( 7.1) и ( 7.2) приведены в приложении П.
7.2. При коэффициенте стеснения потока поперечными сооружениями d > 0,15 глубину местного размыва у такого сооружения следует определять согласно рекомендациям в разделе 6 как у плохо обтекаемых струенаправляющих дамб.
7.3. Скорость потока υ г , м/с, в голове поперечного сооружения или боковой грани береговой опоры следует определять в зависимости от расчетной ширины и направления набегающего потока на сооружение по формулам:
при a ³ 4 5 ° υ г = (b / H)1/4 υ ; (7.3)
при a < 4 5 ° 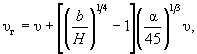 (7.4)
(7.4)
где υ - скорость потока в расчетных условиях на вертикали в голове поперечного сооружения до его постройки или у подошвы конуса в створе моста после общего размыва, м/с.
При определении скорости потока υ г по формулам ( 7.3) и ( 7.4) при b / H > 50 или b / H < 1 следует принимать соответственно b / H = 50 и b / H = 1.
7.4. Наибольшую глубину местного размыва в неоднородных по крупности несвязных грунтах у сплошных незатопляемых поперечных сооружений и береговых опор следует определять по формулам:
а) при υ г > 0,45 υ 0D h = hD + 1,3D / p; (7.5)
б) при υ г £ 0,45 υ 0D h = 1,3D / p, (7.6)
где hD - глубина размыва, определяемая по формулам ( 7.1) или ( 7.2), в которых вместо υ 0 принимают υ 0D - размывающую скорость для среднего диаметра частиц отмостки D (см. п. 7.5) при глубине потока Н и K υ = 1.
К расчету следует принимать меньшую из глубин, получаемых по формулам ( 7.5) или ( 7.6) и по формулам ( 7.1) или ( 7.2) для грунта, средний диаметр частиц которого dм определяют по формуле ( 5.21).
7.5. Средний диаметр частиц отмостки D, м, и их содержание в грунте (по массе) р следует определять:
а) в случае, предусмотренном п. 7.4.а, - подбором из уравнений
при b / H ³ 1 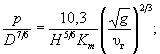 (7.7)
(7.7)
при b / Н < 1 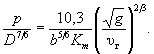 (7.8)
(7.8)
При решении уравнений ( 7.7) или ( 7.8) и назначении расчетных значений D и р поступают, как при расчете размывов у опор в аналогичных условиях, изложенных в приложении Ж;
б) в случае, предусмотренном п. 7.4.б, - по гранулометрическому составу грунта согласно п. 5.2.4. При этом минимальную крупность частиц Dmin, входящих в слой отмостки, следует начинать определять с расчета по формуле
![]() (7.9)
(7.9)
в) при наличии в грунте крупных включений - по среднему диаметру частиц этих включений.
7.6 Наибольшую глубину местного размыва у массивных затопляемых поперечных сооружений высотой Н1 следует определять согласно пп. 7.1 - 7.5 как и у незатопляемых поперечных сооружений с учетом того, что правую часть формулы ( 7.1 ) или ( 7.2 ) умножают, а правую часть уравнений ( 7.7 ) или ( 7.8 ) делят на коэффициент f1, определяемый по формуле ( 5.11 ).
За расчетную глубину местного размыва у затопляемых поперечных сооружений следует принимать наибольшую глубину местного размыва, полученную как при расчетном уровне, когда сооружение затоплено, так и при условиях его работы как незатопленного (например, для шпоры, отжимающей поток от вогнутого берега излучины при прохождении потока в бровках русла). Пример расчета у затопляемой шпоры приведен в приложении П.
7.7 В случае, когда в процессе местного размыва обнажаются слои грунтов различной крупности, наибольшую глубину размыва следует определять с учетом рекомендаций п. 5.4.2 и приложения И:
а) при однородных по крупности слоях с залеганием сверху более мелкого грунта, а также при верхнем более мелком и неоднородном по крупности грунте - по формулам ( 7.1) или ( 7.2) для обнажаемого грунта, а при поступлении наносов в воронку размыва - по меньшему из значений, получаемых по формулам ( 7.1) или ( 7.2) для обнажаемого грунта и влекомого потоком;
б) при однородных по крупности слоях с залеганием слоя из мелкого грунта (со средним диаметром частиц d2) ниже крупного (со средним диаметром частиц d1), а также при нижнем более мелком неоднородном по крупности грунте - по формуле
h = h2 - h d , (7.10)
где h2 - глубина местного размыва, определяемая по формуле ( 7.1) или ( 7.2) для слоя с более мелким (d2) грунтом;
h d - снижение размыва из-за заноса воронки более крупным грунтом d1 верхнего слоя, определяемое по формуле ( И.2) приложения И;
в) при расположении в нижнем слое более крупного неоднородного по составу несвязного грунта следует учитывать его неоднородность.
В случае, предусмотренном в п. 7.4.а и hD ³ D , глубину местного размыва определяют по формуле ( 7.5), в остальных случаях по формуле ( 7.6) с учетом вышележащих слоев [по аналогии с формулой ( И.5)].
Если в воронку размыва поступают наносы (материал верхнего слоя), то необходимо проверить возможность стабилизации размыва при динамическом равновесии частиц верхнего слоя;
г) при расположении в нижнем слое связного грунта - по аналогии с п. 6.2.3.б.
8 Размыв у подошв насыпей и закрепленных берегов русел от продольных течений, волновых воздействий и нарушения естественного хода руслового процесса*
* Все рассматриваемые в главе размывы условно отнесены к местным, хотя некоторые (например, от продольных течений) имеют иную природу образования.
8.1 Возможную глубину размыва h, м, от продольных течений у подошвы насыпи с верховой ее стороны на вертикали с глубиной Н и скоростью потока υ следует определять в зависимости от грунтов в основании насыпи:
а) при однородных несвязных грунтах со средним диаметром частиц d, м
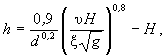 (8.1)
(8.1)
где x - коэффициент, характеризующий увеличение размывов от продольных течений при одновременном воздействии волн (см. п. 8.3); при отсутствии волновых воздействий x = 1;
б) при неоднородных несвязных грунтах, когда υ > υ 0D ,
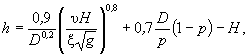 (8.2)
(8.2)
где D, р - диаметр отмащивающих частиц, м, и их содержание по массе в перерабатываемом грунте, определяемые с учетом гранулометрического состава грунта подбором из уравнений:
![]() ( 8.3)
( 8.3)
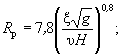 (8.4)
(8.4)
в) при неоднородных несвязных грунтах, когда υ £ υ0D
![]() (8.5)
(8.5)
Полученные по формулам ( 8.2) и ( 8.5) глубины размыва не должны быть больше глубин, определяемых по формуле ( 8.1) для мелких частиц грунта со средним диаметром частиц dм, который находится по формуле ( 5.21).
Размывающую скорость υ0D для грунтов со средним диаметром частиц D следует определять по приложению А.
г) при связных грунтах
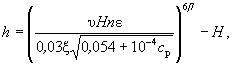 (8.6)
(8.6)
где n - коэффициент шероховатости на рассматриваемом участке проложения насыпи;
e - коэффициент абразивности (см. п. 5.3.2);
с р - расчетное сцепление грунта, Па.
При необходимости учета температурного режима грунта или его засоленности первый член в формуле ( 8.6) следует принимать с коэффициентами соответственно (1 / кt)6/7, (1 / кс)6/7 или (1 / кtкс)6/7 в зависимости от характеристик грунта. Значение коэффициентов кс и кt - см. А.10, А.11;
д) при обнажении в процессе размыва слоя грунта, отличного от вышележащего, расчет размыва в нем производят согласно требованиям п. 5.4.2 в предположении, что рассматриваемый грунт находится на поверхности поймы или русла, по формулам соответственно ( 8.1), ( 8.2) или ( 8.6), а в случае, указанном в п. 8.1.в, по формуле
![]() (8.7)
(8.7)
где å D - толщина вышележащих слоев.
8.2 Глубину размыва h, м, от продольных течений при наличии волновых воздействий у подошвы насыпи, стесняющей русло при долинных ходах на прижимных участках рек, следует определять в зависимости от подстилающих русло грунтов и режима наносов:
а) при отсутствии поступления наносов (случай, предусмотренный п. 4.4.б) расчет следует производить по формулам ( 8.1) - ( 8.7), принимая в качестве Н и υ соответственно глубину и скорость потока у подошвы насыпи до размыва;
б) при движении наносов в русле (случай, предусмотренный п. 4.4.а) расчет размывов в однородных несвязных грунтах следует выполнять по формуле
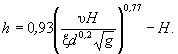 ( 8.8)
( 8.8)
Размыв в неоднородных несвязных, связных и слоистых грунтах следует определять по формулам ( 8.2) - ( 8.7). Причем за расчетную глубину размыва принимают меньшую из глубин, полученных по указанным формулам для соответствующего случая. Для частиц dн, равных среднему диаметру частиц донных наносов в русле, расчет ведут по формуле ( 8.8).
В формулах ( 8.2) - ( 8.8) Н и υ - соответственно глубина и скорость потока у подошвы насыпи до размыва с учетом возможных естественных преобразований в русле.
Пример расчета глубины размыва для случаев, рассматриваемых в пп. 8.1 и 8.2, приведены в приложении Р.
8.3. Глубину размыва у подошвы насыпи от продольных течений при наличии волновых воздействий следует определять по соответствующим формулам ( 8.1 ), ( 8.2 ), ( 8.4 ), ( 8.6 ) и ( 8.8 ), в которых коэффициент x , характеризующий дополнительное «обезвешивание» частиц грунта при волновых воздействиях, равен
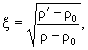 (8.9)
(8.9)
где ρ, ρ' - фактическая и «обезвешивающая» плотность частиц грунта;
ρ 0 - плотность воды.
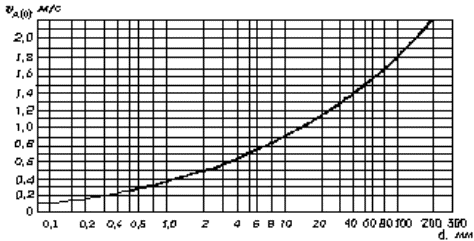
Рисунок 8.1. - График размывающих донных скоростей.
Обезвешивание частиц при волновых воздействиях количественно можно оценивать по зависимости
![]() (8.10)
(8.10)
где hв, Т - высота, м, и период, с, волны;
к - размерный коэффициент, равный 2 м/с0,5.
8.4 Возможную глубину размыва h от волновых воздействий у подошвы насыпи определяют по приложению С из уравнения
υdmax £ υd(0), (8.11)
где υdmax - максимальная донная скорость нисходящего с откоса потока от действия волн у подошвы насыпи;
υd(0) - размывающая донная скорость для грунтов в основании насыпи (см. п. 8.5).
8.5 Размывающую донную скорость υd(0) следует принимать по графику (рисунок 8.1 ) в зависимости от среднего диаметра частиц несвязного грунта d (неоднородность несвязного грунта не учитывается) или эквивалентного диаметра связного материала, мм, определяемого по формуле
d э = 7,5(0,1 + 10cр), (8.12)
где cр - расчетное сцепление, 105 Па.
8.6 При совместных воздействиях продольных течений и волн к расчету следует принимать наибольшие глубины размыва, полученные только от волновых воздействий (см. п. 8.4) или от расчетных продольных течений при наличии волн (см. п. 8.1 - 8.2). В указанных расчетах следует принимать расчетные параметры волн.
Поскольку подмыв подошвы насыпи нельзя допускать, полученные глубины размыва характеризуют тип и мощность укрепления, необходимого для защиты от размыва основания насыпи.
8.7 Местные размывы у подошвы насыпи со стороны вогнутого берега вызываются нарушением естественного хода руслового процесса при воздействии искривленного потока (в плане и поперечном сечении) с неразмываемым речным откосом.
Глубину местного размыва у подошвы насыпи h, м, возникшего в связи с нарушением естественного хода руслового процесса, следует определять по формуле
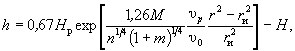 (8.13)
(8.13)
где Нр, υр - средняя глубина, м, и скорость, м/с, потока в рассматриваемом створе русла (после стеснения) при расчетном уровне;
υ0 - размывающая скорость для размываемого грунта на вертикали с глубиной Нр, м/с;
n - коэффициент шероховатости укрепления, определяемый в зависимости от материала укрепления (для плитных укреплений n = 0,011 - 0,015; для каменной наброски n = 0,03 - 0,045);
М - коэффициент формы укрепления, принимаемый для вертикальных стенок и стенок с заложением откоса m < 1, а также без фундамента (например, каменная наброска) равным 1,0; для откосного типа укрепления (при крутизне откоса m ³ 1) с вертикальной внешней стенкой фундамента М = 1,2;
r и , r - минимальный радиус кривизны излучины соответственно по оси излучины и у вогнутого берега (см. приложение Т);
Н - глубина потока у вогнутого берега (после стеснения) при расчетном уровне, м.
Пример расчета по формуле ( 8.13) приведен в приложении Т.
8.8 Глубину местного размыва у закрепленного вогнутого берега излучины следует определять по формуле ( 8.13 ). При этом, если со стороны вогнутого берега есть пойменный массив (т.е. в паводки вода выходит на пойму), то глубину местного размыва у закрепленного берега следует определить как при расчетном уровне, так и при условиях, когда вода достигла бровки берега. К расчету принимают наибольшую глубину местного размыва.
Приложение А
(обязательное)
РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ НАНОСОВ И ГРУНТОВ
А.1 При расчете русловых деформаций грунты подразделяются на несвязные и связные, талые и оттаявшие.
В расчетах к оттаявшим относят только связные грунты, в которых после промерзания нарушаются внутренние связи. Все несвязные грунты при оттаивании практически не меняют своих физико-механических свойств и относятся поэтому к талым.
Далее, если не оговаривается, рассматриваются характеристики талых грунтов.
А.2 К несвязным грунтам относятся крупнообломочные (валунный, галечниковый, гравийный) и песчаные грунты, не обладающие свойством пластичности (раскатывания).
При расчете местных размывов к несвязным следует относить указанные грунты, содержащие по массе: не более 10 % растительных остатков (торф); б) пылеватые пески с содержанием пылеватых частиц (мельче 0,10 мм) менее 20 %.
А.3 При расчетах размывов основной (интегральной) характеристикой несвязного грунта является средний диаметр частиц d, определяемый на основе механического (ситового) анализа по формуле
![]() (А.1)
(А.1)
где di - средний диаметр частиц i-й фракции, определяемый среднеарифметическим размером отверстий сит, ограничивающих данную фракцию;
pi - содержание в грунте i-й фракции, в долях единицы по массе;
n - число фракций.
Если несвязный грунт содержит частицы мельче 0,10 мм, то к расчету принимают средний диаметр частиц грунта крупнее 0,10 мм, вычисляемый по формуле
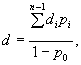 (А.2)
(А.2)
где p0 - содержание в грунте частиц мельче 0,10 мм, в долях единицы.
Значения pi и di определяют на основании гранулометрического анализа проб грунта, отобранных в местах предполагаемых местных размывов. При этом за массу всего несвязного грунта принимают массу без растительных остатков.
А.4 Несвязный грунт считается однородным при соблюдении любого из (достаточных) условий:
а) Dmax / d £ 3; (А.3)
б) в случае, предусмотренном п. 4.4.а, при средней скорости потока больше размывающей для частиц диаметром Dmax.
Здесь Dmax - средний диаметр крупных частиц, которые составляют 2 % массы грунта, или самой крупной (по размеру) фракции, если она составляет 2 % и более массы грунта;
Когда самая крупная по размеру частиц фракция составляет менее 2 % массы грунта, средний диаметр крупных частиц определяют по формуле
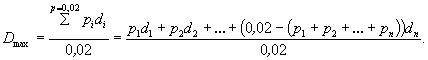 (А.4)
(А.4)
где p1 - содержание по массе в грунте самой крупной фракции со средним диаметром частиц d1;
p 2 , pn - содержание по массе следующих по крупности фракций со средним диаметром частиц d2 и dn.
А.5 Несвязный грунт следует относить к неоднородному, если:
а) частиц со средним диаметром D, образующих отмостку на дне воронки, не менее 2 %, и они удовлетворяют неравенству
D / d > 3.
Примечание. Расчет среднего диаметра частиц слоя отмостки D приведен в разделах основного текста для каждого вида сооружений в зависимости от гранулометрического состава грунта и гидравлических характеристик потока;
б) имеются крупные включения не менее 2 % массы грунта, когда средняя скорость потока меньше размывающей для среднего диаметра частиц D этих включений.
К материалу, содержащему крупные включения со средним диаметром D = Dmax, относится грунт, удовлетворяющий неравенству Dmax / dм ³ 25, где dм - средний диаметр частиц материала без крупных включений. Примером крупных включений служит галька (Dmax) в песке (dм).
А.6 При расчете местных размывов основной характеристикой связного грунта является расчетное удельное сцепление (или расчетное сцепление) ср, определяемое по формуле
![]() (А.5)
(А.5)
где cн - нормативное сцепление, определяемое на основании стандартных методов испытаний (согласно ГОСТ 20522-75 или заменяющего его документа) в состоянии капиллярного водонасыщения при полной влагоемкости;
g g - коэффициент надежности по грунту, учитывающий вероятность отклонения величины сил сцепления от нормативного значения и определяемый с учетом доверительной вероятности 0,90; при отсутствии данных испытаний образцов грунта можно принимать максимальное значение g g = 2.
При отсутствии данных инженерно-геологических исследований допускается определять расчетное удельное сцепление cр связных грунтов по СНиП 2.02.01-83 или заменяющим его нормативным документам, а при высокой заторфованности связных грунтов - по таблице А.1.
Единица измерения сцеплений - паскаль (Па).
А.7 Если в полевых условиях получено нормативное сцепление оттаявшего грунта cн(от), то для перехода к соответствующему значению талого грунта можно воспользоваться формулой
c н = K р с н(от) , (А.6)
где коэффициент перехода K р принимают равным 1,5 при нормативном значении показателя текучести 0,25 £ Il £ 0,75 и равным 1,1, если значение Il выходит из указанного диапазона.
Таблица А.1 - Расчетное сцепление заторфованного связного грунта
|
Содержание растительных остатков в грунте, %, по массе |
Вид торфа |
Расчетное сцепление cр, 105 Па |
|
Более 60 |
Древесный |
0,005 |
|
Хвощевой |
0,025 |
|
|
40 - 60 (сильнозаторфованный) |
Осоковогипновый |
0,025 |
|
Сфагновый |
0,40 |
|
|
25 - 40 (среднезаторфованный) |
Осоковогипновый |
0,075 |
|
Сфагновый |
0,10 |
Нормативное
значение показателя текучести грунтов ![]() определяют в
зависимости от природной влажности W
и числа пластичности Wп = Wт - Wр, где Wт,
Wр - влажность грунта на
границах текучести и раскатывания (в долях единицы).
определяют в
зависимости от природной влажности W
и числа пластичности Wп = Wт - Wр, где Wт,
Wр - влажность грунта на
границах текучести и раскатывания (в долях единицы).
Коэффициент надежности по грунту g g , полученный для оттаявшего монолита, следует принимать в качестве искомого при определении расчетного сцепления талого грунта.
А.8 Размывающей (средней на вертикали с глубиной потока Н) скоростью потока υ0 для данного грунта называют минимальную среднюю скорость, при которой появляются первые признаки размыва дна водотока.
При отсутствии специальных обоснований размывающую скорость следует определять в предположении, что на пойменных участках дерновой покров отсутствует (разрушен при производстве работ).
Размывающую скорость υ0, м/с, для однородного несвязного грунта со средним диаметром частиц d, м, при глубине потока Н, м, рекомендуется определять по формуле
![]() (А.7)
(А.7)
где g - ускорение свободного падения (g = 9,8 м/с2).
По этой же формуле требуется определять размывающую среднюю скорость υ0D для частиц слоя отмостки и i-го слоя грунта, заменяя в формуле средний диаметр частиц d средними диаметрами частиц соответственно слоя отмостки D и i-го слоя грунта di.
Для ускорения расчета по формуле ( А.7) рекомендуется пользоваться графиком (рисунок А.1).
Для пылеватых песков, содержащих пылеватых частиц (в долях единицы по массе) 0,03 £ pп < 0,20, размывающую скорость следует определять по формуле
![]() (А.8)
(А.8)
Для засоленных песчаных грунтов (средний диаметр частиц до 2 мм) размывающую скорость определяют по формулам ( А.7) или ( А.8) с коэффициентом 0,92.
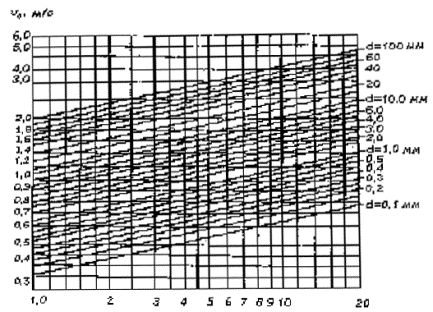
Рисунок А.1 - График для определения размывающей скорости несвязных грунтов
А.9 Размывающую скорость для связных грунтов, м/с, рекомендуется определять по формуле
![]() (А.9)
(А.9)
где С - коэффициент Шези, определяемый в зависимости от глубины потока Н и коэффициента шероховатости n: можно принимать С = Н1/6 / n.
c р - расчетное сцепление, Па.
Для ускорения расчета по формуле ( А.9) составлен график размывающей скорости при коэффициенте шероховатости n = 0,03 (рисунок А.2). При n ¹ 0,03 значения υ0, полученные по графику, следует умножать на величину 0,03 / n.
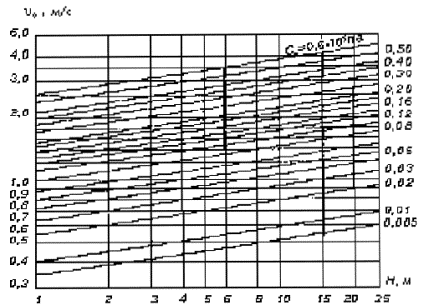
Рисунок А.2 - График для определения размывающей скорости связных грунтов при коэффициенте абразивности e = 1 и коэффициенте шероховатости n = 0,03
А.10 Для связных засоленных грунтов, содержащих менее 3 % легкорастворимых солей, размывающую среднюю скорость потока следует определять по формуле
υ0с = υ0кc, (А.10)
где υ0 - размывающая средняя скорость, определяемая по формуле ( А.9);
к с - понижающий коэффициент, который допускается принимать в зависимости от расчетного сцепления равным:
с р × 105 Па £ 0,05 0,01 0,02 0,03
к с 0,92 0,90 0,90 0,75
с р × 105 Па 0,04 0,05 0,075 ³ 0,010
к с 0,72 0,67 0,63 0,59
При содержании в грунте свыше 3 % легкорастворимых солей размывающая скорость должна устанавливаться на основании специальных исследований.
А.11 Размывающую скорость для оттаявших связных грунтов следует определять по формуле
υ 0 t = υ 0 к t , (А.11)
где кt - коэффициент уменьшения размывающей скорости потока для оттаявших грунтов по сравнению с талыми, определяемый по таблице А.2, в зависимости от вида криогенной текстуры грунта в мерзлом состоянии и льдистости за счет ледяных включений* (т.е. отношения объема ледяных включений к объему мерзлого грунта).
* Указанную льдистость следует отличать от суммарной льдистости (отношение объема льда к объему мерзлого грунта).
Таблица А.2 - Значения коэффициента кt
|
Вид криогенной текстуры |
Льдистость за счет ледяных включений |
кt |
|
Атакситовая |
Более 0,5 |
0,3 |
|
Слоисто-сетчатая |
0,4 - 0,03 |
0,3 - 0,5 |
|
Массивная |
0,03 и менее |
0,5 - 0,9 (0,75 - 1) |
|
Примечания: 1. В таблице А.2 меньшее значение кt соответствует большей льдистости за счет ледяных включений. 2. Значения кt приведены для связных грунтов, в скобках - для пылеватого песка с содержанием пылеватых частиц от 20 до 70 %. |
||
Для оттаявших засоленных грунтов размывающую скорость определяют по формуле
υ 0 t c = υ 0 к t к c . (А.12)
А.12 Гидравлическую крупность частиц несвязного грунта ω (т.е. скорость их осаждения в стоячей воде) следует определять в зависимости от диаметра частиц d по графику (рисунок А.3).
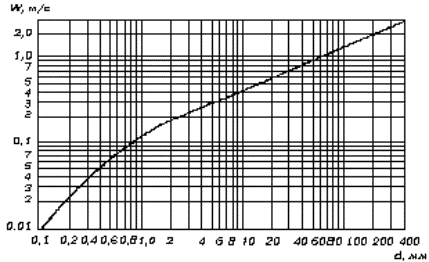
Рисунок А.3 - График для определения гидравлической крупности несвязных грунтов
Гидравлическую крупность несвязного грунта, состоящего из частиц различной крупности, определяют как средневзвешенную по аналогии с определением среднего диаметра частиц грунта по формуле ( А.1) или ( А.2).
А.13. Гидравлическую крупность отрывающихся отдельностей связного грунта принимают по таблице А.3 в зависимости от их толщины z, определяемой по формуле ( 5.27).
А.14. Для пылеватых песков с содержанием пылеватых частиц pп ³ 0,2 (грунт относится к связному) гидравлическую крупность следует определять по эквивалентному расчетному сцеплению, Па
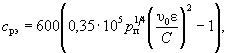 (А.13)
(А.13)
где υ0 - размывающая скорость для песчаных частиц грунта, м/с, определяемая по формуле ( А.7);
С - коэффициент Шези, м0,5/с;
e - коэффициент абразивности, принимаемый равным 1,16 при грядовом движении по руслу песчаного материала, при отсутствии движения песчаного материала e = 1.
Если по формуле ( А.13) получается cрэ < 0,001 × 105 Па, то рекомендуется принимать cрэ = 0,001 × 105 Па.
Таблица А.3 - Гидравлическая крупность отрывающихся отдельностей связного грунта
|
Расчетное сцепление cр, 105 × Па |
Толщина отрывающихся отдельностей z, мм |
Гидравлическая крупность ω, м/с |
|
0,001 |
0,36 |
0,067 |
|
0,005 |
0,38 |
0,07 |
|
0,01 |
0,41 |
0,077 |
|
0,025 |
0,50 |
0,086 |
|
0,050 |
0,65 |
0,10 |
|
0,075 |
0,80 |
0,11 |
|
0,10 |
0,91 |
0,12 |
|
0,25 |
1,85 |
0,15 |
|
0,50 |
3,35 |
0,20 |
|
0,75 |
4,85 |
0,25 |
|
1,0 |
6,35 |
0,31 |
Приложение Б
(обязательное)
КОЭФФИЦИЕНТ ФОРМЫ СВАЙНЫХ ФУНДАМЕНТОВ
Б.1 Под коэффициентом формы М свайного фундамента понимают коэффициент увеличения местного размыва у ряда свай по сравнению с размывом у одной сваи цилиндрической формы.
Коэффициент формы М следует определять у расчетного ряда, в качестве которого необходимо принимать один из первых двух рядов свайного фундамента с наибольшей глубиной размыва и расположенного при a £ 20 ° перпендикулярно продольной оси опоры, а при a > 20 ° вдоль ее (рисунок Б.1).
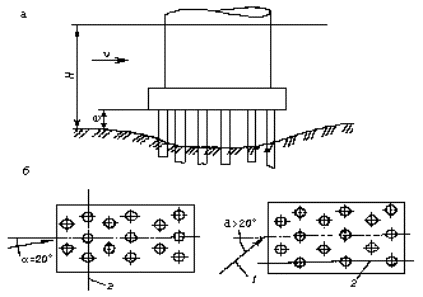
Рисунок Б.1 - К определению расчетного ряда свайного фундамента:
а - продольный вид опоры; б - план свай;
1 - направление течения; 2 - расчетный ряд
При одинаковых форме и размерах свай в двух рассматриваемых рядах, а также одинаковых просветах между сваями расчетным будет тот ряд, в котором находится больше свай.
Б.2 Коэффициент формы М свайного фундамента с количеством свай n > 1 в расчетном ряду следует определять по формуле
M = M1M2cMnc, ( Б .1)
где М1 - коэффициент формы отдельной сваи, принимаемый согласно п. 5.1.9;
М 2с - коэффициент увеличения размыва у двух свай по сравнению с размывом у отдельной сваи
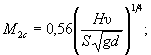 (Б.2)
(Б.2)
Мn с - коэффициент увеличения размыва у n свай по сравнению с размывом у двух свай
![]() (Б.3)
(Б.3)
S - расстояние в свету между сваями в ряду, м;
Шn , Ш2 - полная ширина ряда из n свай и из двух свай (рисунок Б.2).
Коэффициент М2с рассчитывают по формуле ( Б.2) при всех несвязных грунтах по среднему диаметру частиц d, м; при связных - по утроенной толщине отрывающихся отдельностей (т.е. d = 3z); в слоистых грунтах - по вскрываемому грунту.
Значения коэффициентов М2с и Мnс принимают:
при M2c £ 1 M2c = Mnc = 1;
при M2c ³ 1,75 / M 1 M2c = 1,75 / M 1 ;
при М2сМnc ³ (1,1 / M 1 ) n 2/3 M2cMnc =(1,1 / M 1 ) n 2/3 .
При неодинаковых просветах между сваями в расчетном ряду коэффициенты М2с и Мnс определяют с учетом наибольшего просвета Smax (см. рисунок Б.2) по формулам
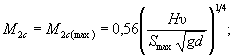 (Б.4)
(Б.4)
![]() (Б.5)
(Б.5)
Произведение М2с(max)Мnс(max) необходимо сопоставить с коэффициентом увеличения размыва М2с(min) у двух свай в ряду, расположенных с минимальным просветом Smin. К расчету по формуле ( Б.1) следует принимать наибольшее значение из сопоставляемых величин. При этом, если М2с(max)Мnc(max) < Мnc(min), то принимают Мnc = 1.
При наличии наклонных свай в плоскости, перпендикулярной направлению сечения, к расчету следует принимать среднюю величину просвета S между ними на уровне выше отметки общего размыва (рисунок Б.3, а), а в случае, когда низ плиты ростверка заглублен ниже отметки общего размыва - расстояние между сваями в месте примыкания к плите ростверка (рисунок Б.3, б).
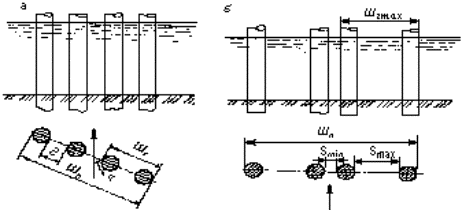
Рисунок Б.2 - Основные геометрические размеры свайных рядов:
а - ряд с одинаковыми просветами между сваями; б - ряд с неодинаковыми просветами
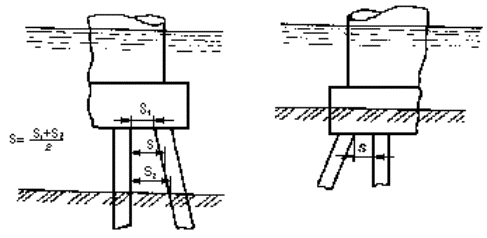
Рисунок Б.3 - Часть фасада опор с наклонными сваями фундамента
Приложение В
(справочное)
ЗНАЧЕНИЯ ПРИВЕДЕННОЙ ШИРИНЫ b a ХАРАКТЕРНЫХ ФОРМ ОПОР
Формулы для определения приведенной ширины b a некоторых характерных форм опор (или их элементов) даны в таблице В.1. Формулы не учитывают возможной скошенности или закругления вершины двугранного угла Q , которыми в расчетах приведенной ширины опоры можно пренебречь.
Характерные формы опор представлены на рисунке В.1.
Таблица В.1 - Формулы для приведенной ширины опоры
|
№ схемы на рисунке В.1 |
Форма тела опоры |
Расчетные формулы |
|
1 |
Прямоугольная |
b a = Lsin a + bcos a |
|
2 |
Прямоугольная с закругленными углами при радиусе закругления r |
b a = (L - 2r)sin a + b |
|
3 |
Полуциркульная |
b a = (L - b)sin a + b |
|
4 |
Полуциркульная с двугранным углом в лобовой части |
при a < Q/2 при a ³ Q/2 |
|
5 |
Прямоугольная с двугранным углом в лобовой части |
при α < Θ/2 при a ³ Q/2 |
|
6 |
Прямоугольная с двугранным углом в лобовой и торцевой частях |
при a < Q/2 при |
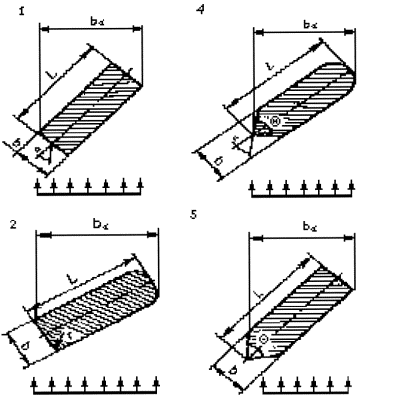
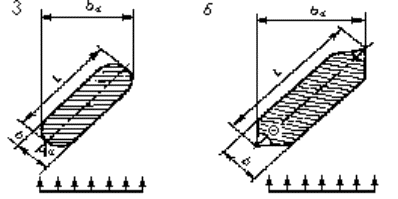
Рисунок В.1 - Характерные формы опор
Приложение Г
(справочное)
ПРИМЕРЫ РАСЧЕТА МЕСТНОГО РАЗМЫВА У ПРОМЕЖУТОЧНЫХ ОПОР МОСТОВ
Пример Г.1 Глубина и средняя скорость перед опорой после общего размыва Н = 6 м и υ = 1,25 м/с. Дно реки сложено мелкозернистым песком, гранулометрический состав которого приведен ниже:
Диаметр частиц, мм > 0,1 0,1 - 0,25 0,25 - 0,50 0,50 - 1,00 1 - 2 2 - 3
Содержание pi,
по массе, % 2,15 23,61 53,26 16,02 3,57 1,39
Определить глубину местного размыва у овальной в плане опоры шириной b = 4 м и длиной L = 12 м (см. рисунок 5.1). Опора расположена под углом a = 15 ° к направлению течения.
Решение . 1. Определяем неоднородность грунта. Самая крупная фракция составляет менее 2 % массы грунта. Поэтому по формуле ( А.4) средний диаметр крупных частиц грунта:
![]()
По формуле ( А.2) средний диаметр частиц грунта:
![]()
Имеем Dmax / d = 2,2 / 0,46 = 4,8, что больше 3, т.е. не соблюдается одно из условий однородности грунта согласно п. А.4 .
Проверяем второе условие. Размывающая скорость для частиц диаметром 2,2 мм по графику (см. рисунок А.1) υ 0 Dmax = 1,23 м/с, что меньше скорости течения. Следовательно, грунт в рассматриваемых условиях отмостки не образует, и расчет выполняем как для однородного грунта со средним диаметром частиц 0,46 мм.
2. Поскольку υ > υ0 (так как даже υ > υ 0 Dmax ) глубину местного размыва определяем по формуле ( 5.1), в которой неизвестны параметры υв, M и K .
3. При гидравлической крупности грунта со средним диаметром частиц 0,46 мм ω = 0,06 м/с (см. рисунок А.3) и взмучивающая скорость по формуле ( 5.7) υв = (9,8 × 0,06 × 6)1/3 = 1,52 м/с.
Примечание. Более правильным является определение гидравлической крупности как средневзвешенной по аналогии с определением среднего диаметра частиц грунта по формуле ( А.2); тогда получается ω = 0,046 м/с и υв = 1,4 м/с.
4. По п. 5.1.9 коэффициент формы овальной опоры M = 0,85.
5. Для определения коэффициента косины K вначале по приведенным в приложении В формулам получим при a = 15 ° приведенную ширину опоры:
b a = (L - b)sin a + b = (12 - 4)sin 15 ° + 4 = 6,07 м .
По рисунку 5.7 или по формуле ( 5.13), поскольку b a / b < 2,53M1/3 имеем:
![]()
6. Глубина местного размыва по формуле ( 5.1):
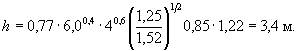
Пример Г.2 Для условий примера Г.1 определить глубину местного размыва у опоры на массивном фундаменте, состоящей из двух элементов овальной формы в плане: нижняя часть возвышается над дном на высоту H1 = 2,0 м, как в примере Г.1 (b1 = 4 м, L1 = 12 м), верхняя имеет b2 = 3 м и L2 = 11 м (см. рисунок 5.2 , б).
Решение . Расчет местного размыва производим по формуле ( 5.3), в которой неизвестен только параметр F(b), учитывающий геометрию опоры.
1. Элементы опоры в плане овальной формы, поэтому они имеют одинаковый коэффициент формы М 1 = М2 = 0,85 (см. п. 5.1.9).
2. Коэффициент косины для первого элемента определен в примере Г.1 и равен K 1 = 1,22. Аналогично для второго элемента
bα2 = (11 - 3)sin 15 ° + 3 = 5,07 м ;
![]()
3. По формуле ( 5.11) при Н1 / Н = 2 / 6 = 0,334 > 0,3
А 1 = 1 и j 1 = 1/3 f1
= ![]() = 0,695.
= 0,695.
По формуле ( 5.12), в которой Аn - 1 = А2 = А1 и j 2 = j 1 ,
f 2 = 1 - 0,695 = 0,305.
4. По формуле ( 5.5)
F (b) = 40,6 × 0,85 × 1,22 × 0,695 + 30,6 × 0,85 × 1,39 × 0,305 = 1,65 + 0,70 = 2,35.
5. Подставляя в формулу ( 5.3) результаты проведенного расчета и полученные в примере Г.1, определим глубину местного размыва:
h =
0,77 × 6,00,4 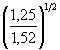 · 2,35 = 3,28 м.
· 2,35 = 3,28 м.
Пример Г.3 Для условий примера Г.1 определить глубину местного размыва у опоры на свайном основании (см. рисунок 5.4, а и б):
Число свай-оболочек диаметром b1 = 1,2 м по фасаду n = 2, просвет по фасаду между сваями S = 1,5 м; плита ростверка прямоугольной формы в плане, шириной по фасаду b2 = 5,0 м и длиной L2 = 12 м; низ плиты ростверка расположен выше отметки дна после общего размыва на е = 0,5 м, толщина плиты ростверка r = 1,5 м; тело опоры овальной формы в плане, шириной и длиной соответственно b3 = 3 м и L3 = 11 м.
Решение . Поскольку е < 0,3Н, расчет глубины размыва следует производить по формуле ( 5.6). Расчет сводится к определению глубины размыва hе у опоры при положении низа ростверка относительно дна после общего размыва, равном е = 0,3Н (см. рисунок 5.5, а), и глубины размыва hм у опоры на массивном фундаменте, по форме в плане соответствующей плите ростверка и с отметкой верха, равной отметке верха плиты (см. рисунок 5.5, в).
Для указанных глубин размыва постоянным является параметр, характеризующий гидравлические характеристики потока.
F (Н, υ) = 0,77Н0,4 ![]() = 0,77 × 6,00,4
= 0,77 × 6,00,4 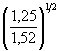 = 1,43.
= 1,43.
Для проводимых расчетов глубин размыва общими являются также коэффициенты формы и косины элементов опор.
1. Коэффициент формы свайного основания определяем по приложению Б:
- коэффициент формы отдельной сваи цилиндрической формы М = 1 (см. п. 5.1.9);
- коэффициент увеличения размыва у двух свай по сравнению с размывом у отдельной сваи по формуле ( Б.2):
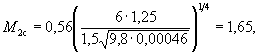
что меньше 1,75, поэтому полученную величину принимаем за искомую. По формуле ( Б.1) коэффициент формы свайного фундамента или 1-го элемента опоры М1 = 1 × 1,65 = 1,65.
Коэффициент косины свайного основания следует принимать K 1 = 1 (см. п. 5.1.10).
2. Коэффициент формы плиты ростверка (или массивного фундамента) М2 = 1,24 (см. п. 5.1.9).
Приведенная ширина плиты ростверка (или массивного фундамента) по приложению В
bα2 = L2sin 15 ° + b2cos 15 ° = 12sin 15 ° + 5cos 15 ° = 3,11 + 4,82 = 7,93 м .
При ![]() = 1,585 и M2 = 1,24 находим по рисунку 5.7 K 2 = 1,1.
= 1,585 и M2 = 1,24 находим по рисунку 5.7 K 2 = 1,1.
3. Коэффициенты формы и косины тела опоры (овальной формы) равны соответственно М3 = 0,85 и K 3 = 1,39 (получено в примере Г.2).
4. Для опоры на свайном основании при е = 0,3Н = 0,3 × 6 = 1,8 м весовые коэффициенты элементов опоры равны:
- для свайного основания при А1 = 1 и j 1 = 1/3 по формуле ( 5.11)
![]()
- для плиты ростверка по формуле ( 5.10) при Аi - 1 = Ai = 1, j i - 1 = j i = 1/3, Hi - 1 = 1,8 м и Hi = 0,3H + r = 1,8 + 1,5 = 3,3 м
f 2 = ![]() - 0,67 = 0,82 - 0,67 = 0,15;
- 0,67 = 0,82 - 0,67 = 0,15;
- для тела опоры по формуле ( 5.12)
f 3 = 1 - 0,82 = 0,18.
5. Параметр F(b) для опоры на свайном основании при е = 0,3Н по формуле ( 5.5)
F (b) = 1,20,6 × 1,65 × 1 × 0,67 + 5,00,6 × 1,24 × 1,1 × 0,15 + 3,00,6 × 0,85 × 1,39 × 0,18 = 1,235 + 0,54 + 0,41 = 2,185.
Глубина местного размыва у такой опоры hе = F(Н, υ) F(b) = 1,43 × 2,185 = 3,12 м.
6. Опора на массивном фундаменте имеет два элемента: фундамент и тело опоры.
Весовой
коэффициент фундамента при ![]() по формуле ( 5.11)
(A1 = 1; j 1 = 1/3) f1 = 0,3341/3 = 0,695.
по формуле ( 5.11)
(A1 = 1; j 1 = 1/3) f1 = 0,3341/3 = 0,695.
Весовой коэффициент тела опоры по формуле ( 5.12) f2 = 1 - 0,695 = 0,305.
7. Параметр F(b) для опоры на массивном фундаменте по формуле ( 5.5)
F (b) = 50,6 × 1,24 × 1,1 × 0,695 + 30,6 × 0,85 × 1,39 × 0,305 = 2,5 + 0,69 = 3,19.
Глубина размыва у такой опоры hм = 1,43 × 3,19 = 4,56 м.
8. Искомая глубина местного размыва по формуле ( 5.6)
h =
3,12 + (4,56 - 3,12) ![]() = 3,12 + 0,44 = 3,56
м.
= 3,12 + 0,44 = 3,56
м.
Пример Г.4 Для условий примера Г.2 определить глубину местного размыва у опоры, если известно, что в русле, коэффициент шероховатости которого n = 0,028, на глубине D = 1 м ниже отметки общего размыва залегают глины с расчетным сцеплением ср = 0,09 × 105 Па.
Решение . 1. Вначале определим по формуле ( А.9) или графику (см. рисунок А.2) размывающую скорость для глин с расчетным сцеплением ср = 0,09 × 105 Па при глубине потока Н = 6 (при определении размывающей скорости глубина потока отсчитывается от отметки общего размыва независимо от того, на какой отметке ниже общего размыва залегает рассматриваемый грунт).
По графику (см. рисунок А.2) размывающая скорость определена равной 1,4 м/с. Поскольку шероховатость русла отличается от той, для которой составлен график (n = 0,03), то фактическая размывающая скорость согласно п. А.9 будет равна υ0 = 1,4 · 0,03 / 0,028 = 1,5 м/с.
2. По таблице А.3 получим две другие необходимые характеристики связного грунта: толщину отрывающихся отдельностей z = 0,87 мм и гидравлическую крупность этих отдельностей ω = 0,12 м/с. Тогда по формуле ( 5.7) взмучивающая скорость равна υв = (9,8 × 0,12 × 6,0)1/3 = 1,92 м/с.
3. По формуле ( 5.8) определим начальную скорость υн, в которой для связных грунтов вместо среднего диаметра частиц несвязного грунта следует принимать (см. п. 5.3.2) d = 3z = 3 × 0,87 = 2,61 мм.
Поскольку опора состоит из двух элементов, расчетную ширину опоры для определения начальной скорости найдем по формуле ( 5.9), в которой b1 = 4,0 м и f1 = 0,695, b2 = 3,0 м и f2 = 0,305 (см. расчет примера 2).
b = (4,00,6 × 0,695 + 3,00,6 × 0,305)5/3 = (2,18)5/3 = 3,36 м.
При ![]()
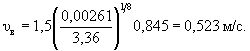
Полученная начальная скорость принята за искомую, так как υн < 0,9υ0 (см. п. 5.1.6).
4. С учетом того, что коэффициент абразивности e = 1,16, так как в воронку размыва поступают песчаные наносы (см. п. 5.3.2), а параметр F(b) = 2,35 (см. расчет примера Г.2), глубина местного размыва в обнажаемой глине (она будет обнажаться, так как размыв в верхнем слое - песке - больше этого слоя) по формуле ( 5.26) равна
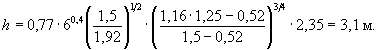
5. При назначении расчетной глубины местного размыва следует учесть следующие два обстоятельства.
Во-первых, полученная глубина размыва в глине больше толщины слоя (а в общем случае - слоев) грунта над глиной, т.е. действительно в процессе местного размыва будет обнажаться нижележащий грунт.
Во-вторых, согласно п. 5.3.3 полученную глубину размыва следует сравнить с глубиной, сформированной наносами. Из примера Г.2 эта глубина равна 3,28 м, что больше рассчитанной для глины. Поэтому искомая глубина h = 3,1 м.
Для рассматриваемого случая, если бы не удовлетворялось первое условие (глубина местного размыва в глине была бы меньше толщины слоя над глиной, т.е. h < D ), то к расчету следовало бы принимать глубину местного размыва h = D (отметка дна воронки размыва равна отметке поверхности глин).
Приложение Д
(рекомендуемое)
УМЕНЬШЕНИЕ ГЛУБИНЫ РАЗМЫВА dт ЗА СЧЕТ СТУПЕНЕЙ НА ГРАНИЦЕ ЭЛЕМЕНТОВ ПРОМЕЖУТОЧНОЙ ОПОРЫ, НАХОДЯЩИХСЯ ВЫШЕ ОТМЕТКИ ОБЩЕГО РАЗМЫВА
В тех случаях, когда выше отметки общего размыва опора имеет ступенчатую форму, можно учесть уменьшение глубины местного размыва, обусловленное наличием ступеней тела опоры или фундамента.
Фактическая глубина размыва будет равна
h т = h - d т . ( Д .1)
Уменьшение размыва от n-го элемента опоры (см. рисунок 5.3) за счет (n - 1) ступеней, находящийся ниже этого элемента, следует определять по формуле:
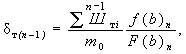 (Д.2)
(Д.2)
где F(b)n - параметр, определяемый по формуле ( 5.5) для всех элементов опоры;
f (b)n = b n 0,6 MnKnfn - параметр, учитывающий геометрию n-го элемента опоры;
![]() - сумма значений
ширины (n - 1) ступеней перед n-ым элементом опоры выше отметки общего
размыва; размеры ступеней принимают без каких-либо поправок на их увеличение
вдоль направления потока со стороны передней (при a £ 20 ° ) или боковой ( a > 20 ° ) грани опоры;
- сумма значений
ширины (n - 1) ступеней перед n-ым элементом опоры выше отметки общего
размыва; размеры ступеней принимают без каких-либо поправок на их увеличение
вдоль направления потока со стороны передней (при a £ 20 ° ) или боковой ( a > 20 ° ) грани опоры;
m 0 - коэффициент заложения откоса с верховой стороны воронки, определяемый по таблице Д.1.
Таблица Д.1 - Коэффициент заложения откоса m0 верховой стороны воронки
|
Грунт |
Диаметр частиц d, мм |
Коэффициент m0 |
|
Несвязный |
|
|
|
Песок: |
|
|
|
мелкий и средний |
0,1 - 0,5 |
1,75 - 1,65 |
|
крупный |
0,5 - 1,0 |
1,65 - 1,60 |
|
Гравий: |
|
|
|
мелкий |
1 - 2 |
1,60 - 1,55 |
|
средний |
2 - 5 |
1,55 - 1,45 |
|
крупный |
5 - 10 |
1,45 - 1,40 |
|
Галька |
10 - 100 |
1,40 - 1,25 |
|
Валуны |
³ 100 |
1,25 |
|
Связный |
< 0,1 |
1,0 |
При учете влияния ступенчатой формы опор на глубину размыва коэффициент m0 следует назначать для всех несвязных грунтов по среднему диаметру (крупности) частиц d, а при слоистом залегании грунтов - по верхнему слою грунта, в качестве которого при движении наносов принимают грунт, влекомый потоком.
Общее снижение размыва от (n - 1)-го элемента опоры (от второго до n-го) за счет ступеней в пределах глубины потока равно сумме уменьшения размыва, приходящегося на каждый элемент опоры:
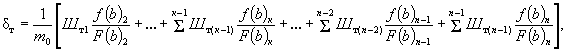
или 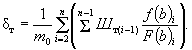 (Д.3)
(Д.3)
Если окажется, что удовлетворяется условие
![]() (Д.4)
(Д.4)
где ![]() - глубина размыва,
приходящаяся на элементы опоры от верхнего до к-го включительно,
- глубина размыва,
приходящаяся на элементы опоры от верхнего до к-го включительно,
то все, что находится выше (к - 1)-й ступени в расчет размыва вводить не требуется. Расчет местного размыва в этом случае производят в предположении, что часть опоры выше (к - 1) ступени отсутствует, и в формуле ( 5.5)
f (b)к, f(b)к+1 ... f(b)n-1 и f(b)n
следует принимать равным нулю (см. пример Д.2).
При недискретном изменении сечения опоры в плоскости, в которой определяют ширину ступеней, такое сечение следует заменить эквивалентным по площади не менее чем тремя одинаковыми по высоте элементами постоянной ширины (см. рисунок 5.6).
Примечание. При расчете глубин местного
размыва слияние ступеней, расположенных на глубине потока выше 0,5Н и имеющих ширину ![]() незначительно и
уменьшение глубины размыва dт можно не учитывать.
незначительно и
уменьшение глубины размыва dт можно не учитывать.
Пример 1. Для условий примера Г.2 определить глубину hт местного размыва у опоры с учетом уменьшения размыва за счет ступени шириной Шт1 = 0,5 м на границе 2-го и 1-го элементов опоры. (Глубина размыва без учета ступеней равна 3,28 м).
Решение . 1. Из примера Г.2 известно, что параметры, учитывающие геометрии всей опоры и только второго элемента соответственно равны F(b)2 = 2,35 и f(b)2 = 0,7.
Для песка со средним диаметром частиц 0,46 мм принимаем по таблице Д.1 коэффициент заложения откоса m0 = 1,65.
2. Подставляя в формулу ( А.2) выявленные выше параметры, получим уменьшение размыва от второго элемента опоры за счет ступени на границе элементов опоры:
![]()
Искомая глубина местного размыва по формуле ( Д.1)
h т = 3,28 - 0,1 = 3,18 м.
Как и следовало ожидать, при относительной ширине ступени Шт1 / b2 = 0,5 / 3 << 0,5 влияние ее на размыв незначительное.
Пример Д.2. Для условий примера Д.1 определить глубину местного размыва у опоры, если ее второй (верхний) элемент представляет собой стойку цилиндрической формы (коэффициенты формы и косины М2 = K 2 = 1) шириной b2 = 1,0 м, а ширина ступени Шт1 = 1,5 м.
Решение . 1. Для такой опоры f(b)2 = 1,00,6 × 1 × 1 × 0,305 = 0,305 и соответственно F(b)2 = 40,6 × 0,85 × 1,22 × 0,695 + 1,00,6 × 1 × 1 × 0,305 = 1,65 + 0,305 = 1,955 м0,6.
2. По формуле ( 5.3) глубина местного размыва (без учета влияния ступени)
h =
0,77 × 60,4 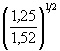 1,955 = 2,79 м.
1,955 = 2,79 м.
3. Для учета
влияния на размыв ступени проверяем условие ( Д.4), в котором ![]() = Шт1 = 1,5 м, а
= Шт1 = 1,5 м, а ![]() = h2 - глубина размыва,
приходящаяся на верхний (второй) элемент опоры:
= h2 - глубина размыва,
приходящаяся на верхний (второй) элемент опоры:
h 2 = 0,77 × 60,4 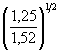 0,305 = 0,44 м.
0,305 = 0,44 м.
Поскольку условие соблюдается (1,5 > 0,44 × 1,65), то при расчете местного размыва в F(b)2 по формуле ( 5.5) f(b)2 = 0 т.е. F(b)2 = f(b)1 = 1,65.
4. Искомая глубина местного размыва по формуле ( 5.3)
h т = 0,77 × 60,4 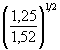 1,65 = 2,35 м.
1,65 = 2,35 м.
Тот же результат получается по формуле ( Д.1): hт = 2,79 - 0,44 = 2,35 м.
Приложение Е
(рекомендуемое)
УМЕНЬШЕНИЕ ГЛУБИНЫ РАЗМЫВА dф ЗА СЧЕТ ОБНАЖАЕМОЙ В ПРОЦЕССЕ МЕСТНОГО РАЗМЫВА ЧАСТИ МАССИВНОГО ФУНДАМЕНТА
Если в процессе местного размыва обнажается часть массивного фундамента, размеры которого в плане больше соответствующих размеров опоры, то такой фундамент уменьшает наибольшую глубину местного размыва h на величину d ф . Фактическая глубина размыва будет равна hф = h - d ф .
Глубину d ф следует определять (рисунок Е.1):
- в грунтах с одинаковыми физико-механическими свойствами при соблюдении неравенства tmax + Шф / m0 £ h - по формуле d ф = Шф / m0;
- в тех же грунтах при несоблюдении указанного неравенства или при слоистом залегании грунтов - графическим путем.
Здесь tmax - глубина заложения (ниже отметки общего размыва) верха наиболее удаленной от тела опоры ступени фундамента;
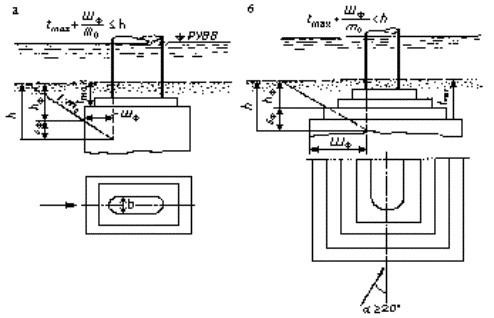
Рисунок Е.1 - К определению глубины уменьшения размыва d ф за счет массивного фундамента в грунтах с одинаковыми физико-механическими свойствами:
а - аналитическим способом; б - графическим
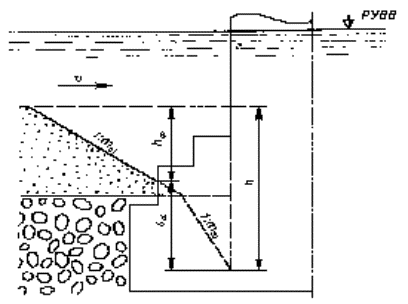
Рисунок Е.2 - К определению снижения размыва d ф в слоистых грунтах
Шф - суммарная ширина ступеней фундамента от ближайшей передней (при a £ 20 °) или боковой (при a > 20 °) грани опоры (или фундамента), располагающейся выше отметки общего размыва; m0 - коэффициент заложения откоса с верховой стороны воронки, определяемый по таблице Д.1 для каждого вскрываемого грунта в процессе местного размыва (рисунок Е.2); для всех несвязных грунтов m0 назначают по среднему диаметру частиц (без учета неоднородности).
При определении уменьшения глубины размыва d ф графическим путем необходимо (см. рисунки Е.1, б и Е.2):
вычертить в масштабе продольное (при a £ 20 ° ) или поперечное (при a > 20 ° ) сечение опоры;
отложить наибольшую глубину местного размыва на вертикали, где наиболее удаленная от оси опоры ее грань пересекает отметку общего размыва;
от полученной таким образом отметки глубины h провести линию верхового откоса, начиная от дна воронки с заложением 1:m0, соответствующем грунту, в котором определялся размыв; при слоистых грунтах заложение откоса 1:m0 в каждом грунте должно соответствовать его физико-механическим свойствам.
По отметке пересечения откоса с фундаментом определяют величину d ф или непосредственно искомую глубину местного размыва.
Примечание. При определении суммарной ширины ступеней фундамента следует:
- ширину ступеней принимать без каких-либо поправок на их увеличение вдоль направления потока при косорасположенных опорах;
- отсчитывать ширину ступеней фундамента от боковой грани опоры (при любом значении угла a), если ступени с этой стороны уже, чем с передней.
Приложение Ж
(рекомендуемое)
ОПРЕДЕЛЕНИЕ СРЕДНЕГО ДИАМЕТРА ЧАСТИЦ СЛОЯ ОТМОСТКИ И ИХ СОДЕРЖАНИЕ В ГРУНТЕ ПРИ РАСЧЕТЕ МЕСТНЫХ РАЗМЫВОВ У ОПОР
В случае, предусмотренном п. 5.2.4, а, для определения характеристик грунта в слое отмостки D и p поступают следующим образом. Принимают некоторое содержание р ³ 0,02 по массе крупных (отмащивающих) частиц в размываемом грунте и для него подсчитывают средний диаметр частиц D по формуле:
![]()
где å pi = p.
Принятое значение p и полученную по формуле величину D подставляют в уравнение ( 5.22). Если окажется p / D > Rp (с точностью ± 5 %), то принимают меньшее значение p, а при p / D < Rp - большее и повторяют те же действия до тех пор, пока подберут значения p и D, удовлетворяющие уравнению ( 5.22).
Если самая крупная фракция со средним диаметром Dmax составляет не менее 2 % массы всего грунта (р ³ 0,02) и удовлетворяет неравенству p / Dmax ³ Rp, то в расчет принимают значения Dmax и p этой фракции.
Если получено p < 0,02, то глубину размыва определяют по формулам для однородного несвязного грунта.
Пример. Для условий примера Г.1 (Н = 6,0 м, υ = 1,25 м/с, опора овальной формы b = 4,0 м, косина потока a = 15 ° ), определить глубину местного размыва, если в процессе общего размыва обнажился гравий средним диаметром частиц d = 3 мм следующего гранулометрического состава:
d , мм 25 - 15 15 - 10 10 - 7 7 - 5 5 - 3
pi , % по массе 1,2 2,4 3,7 6,7 17,2
d , мм 3 - 2 2 - 1 1,0 - 0,5 0,3 - 0,25 0,25 - 0,10
pi , % 31,2 10,8 5,6 17,0 4,2
По руслу влекутся донные наносы - песок со средним диаметром частиц dм = 0,46 мм.
Решение . 1. Определим неоднородность грунта. Самая крупная фракция составляет менее 2 % массы грунта. Поэтому по формуле ( А.4) средний диаметр крупных частиц:
![]()
Имеем ![]() , т.е. грунт может образовывать отмостку.
, т.е. грунт может образовывать отмостку.
Проверяем второе условие. Размывающая скорость для частиц диаметром 17 мм по графику (см. рисунок А.1): υ 0 D max = 2,05 м/с, что больше скорости течения. Следовательно, данный грунт может образовывать отмостку (т.е. он может рассматриваться как неоднородный).
2. Определяем метод нахождения крупности частиц слоя отмостки. Для этого находим:
а) начальную скорость для частиц Dmax по формуле ( 5.8)
при ![]()
υ н D max = 2,05 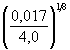 0,895 = 0,905;
0,895 = 0,905;
б) коэффициент абразивности для частиц Dmax при среднем диаметре мелких частиц, в качестве которых следует принимать средний диаметр частиц наносов (см. п. 5.2.3), dм = 0,46 мм, равен e max = 1, так как Dmax / dм = 37 > 30 (см. п. 5.2.3).
Неравенство e max υ > υ н D max удовлетворяется, поэтому средний диаметр частиц слоя отмостки определяем из уравнения ( 5.22).
3. Задаемся содержанием отмащивающих частиц p = 0,02. Для D = Dmax = 17 мм гидравлическая крупность по рисунку А.3 ωD = 0,5 м/с; при Н = 6 м взмучивающая скорость υвD = 3,05 м/с.
По формуле ( 5.19) при М = 0,85 и K = 1,22 находим глубину местного размыва в однородном несвязном грунте со средним диаметром частиц D = Dmax и скорости потока υ = υ0D = 2,05 м/с
h 0D = 0,77 × 60,40,40,6
× 0,85 × 1,22 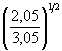 = 3,75
= 3,75 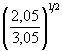 =
3,07 м.
=
3,07 м.
Определяем по ( 5.23) параметр
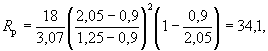 что больше p / D
= 0,02 / 0,017 = 1,18,
что больше p / D
= 0,02 / 0,017 = 1,18,
т.е. уравнение ( 5.22) не удовлетворяется и требуется изменить характеристики отмащивающего грунта.
4. Принимаем в качестве отмащивающих частиц три наибольших по крупности фракции. Тогда p = 0,012 + 0,024 + 0,037 = 0,073;
![]()
Для принятого грунта имеем:
по рисунку А.3 ω D = 0,42 м/с;
по рисунку А.1 υ0D = 1,87 м/с;
по формуле ( 5.7) υвD = 2,9 м/с;
по формуле ( 5.8) υнD = 1,87 ![]() × 0,895 = 0,806 м/с;
× 0,895 = 0,806 м/с;
по формуле ( 5.19)
с учетом, что 0,77H0,4b0,6MK = 3,75, 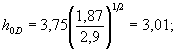
по п. 5.2.3
при ![]() = 25,4 и e = 1,07;
= 25,4 и e = 1,07;
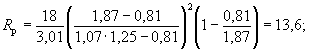
![]()
5. При p = 0,11 D = 9,8 мм. Для такого грунта ω D = 0,41 м/с; υ0D = 1,81 м/с; υвD = 2,8 м/с; υнD = 0,76 м/с;
h 0D = 3,75 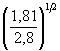 = 3,01;
= 3,01; ![]() и e = 1,075;
и e = 1,075;
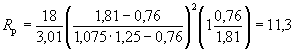 при
при ![]() .
.
Параметры отмащивающего грунта найдены. Он будет отмащивать воронку, так как υ0D > υ и D / d = 9,8 / 3 = 3,26 > 3.
6. По формуле ( 5.16) глубина размыва с учетом образования отмостки
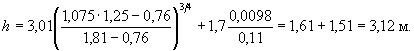
7. Согласно п. 5.3.3 полученную глубину размыва необходимо сопоставить с глубиной размыва в грунте, влекомого потоком. Из примера Г.1 эта глубина равна 3,4 м. Следовательно, к расчету надо принимать глубину размыва 3,12 м.
Как видим, эффект учета неоднородности грунта невелик, что можно было бы прогнозировать, поскольку отношение D / d близко к 3 (критериальной величине).
Глубина размыва в однородном гравии с учетом абразивного воздействия наносов равна 4,98 м, но в этом случае надо было бы принимать к расчету глубину размыва 3,4 м в грунте, влекомым потоком, - песке со средним диаметром частиц 0,46 мм.
Приложение И
(обязательное)
РАСЧЕТ РАЗМЫВОВ У ПРОМЕЖУТОЧНЫХ ОПОР ПРИ СЛОИСТОМ ЗАЛЕГАНИИ ГРУНТОВ
И.1 Расчет размывов при слоистом залегании грунтов зависит от взаимного расположения грунтов, вскрываемых в процессе местного размыва.
Возможны следующие случаи слоистого залегания грунтов:
а) все слои, которые прорезает воронка местного размыва, состоят из однородных несвязных грунтов, причем по мере увеличения глубины местного размыва вскрывается более крупный грунт или все слои состоят из связных материалов;
б) имеется два слоя однородного несвязного грунта, причем вскрывающийся в процессе местного размыва второй слой - более мелкий или такой же по крупности, чем вышележащий;
в) процесс местного размыва проходит в двух слоях несвязного грунта, причем один или оба неоднородные;
г) процесс местного размыва проходит в двух слоях грунта, причем один из слоев - связный грунт;
д) общий случай, когда слоев два и более с произвольным расположением в них грунтов, отличающихся друг от друга по физико-механическим свойствам.
И.2 Для случая, указанного в п. И.1 а, когда поток не влечет донных наносов, глубину местного размыва определяют вначале по формуле ( 5.4 ) для обнажаемого грунта в следующем порядке: находят глубину размыва для первого слоя; если полученная глубина размыва захватывает второй слой, расчет проводят для второго слоя, считая, что он выходит на поверхность, и так до тех пор, пока будет найдет слой, в котором размыв прекратится. Если при расчете для какого-либо слоя глубина размыва получается меньше суммы толщин вышележащих слоев, то это значит, что размыв останавливается на поверхности рассматриваемого слоя.
И.3 В случае, указанном в п. И.1а, когда поток влечет донные наносы, расчет глубины размыва следует производить в таком порядке:
1) определяют глубину размыва hн в грунте dм, влекомом потоком, по формуле ( 5.3);
2) определяют глубины размыва для обнажаемых грунтов согласно рекомендациям п. И.2 по формуле
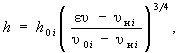 (И.1)
(И.1)
где h0i - глубина размыва, определяемая по формуле ( 5.19) в обнажаемом грунте со средним диаметром частиц di при скорости потока, равной размывающей υ0i для этого грунта;
υ0i, υнi - размывающая и начальная скорости для частиц грунта крупностью di, определяемые для глубины потока Н, т.е. для условий, если бы верх этого слоя находился на отметке после общего размыва.
Коэффициент абразивности e определяют по формуле ( 5.20) с учетом воздействия частиц грунта dм на частицы di;
3) выявляют согласно рекомендациям п. И.2 слой грунта крупностью dj, в котором размыв остановился, и соответствующую глубину размыва hj;
4) сопоставляют глубины размыва hн и hj. Если hн £ hj, то к расчету принимают глубину размыва h = hн. Если hн > hj, то к расчету принимают глубину размыва h = hj.
И.4 В случае, указанном в п. И.1 б, когда поток влечет донные наносы, глубину местного размыва следует определять по формуле ( 5.3 ) или ( 5.6 ) для грунта верхнего слоя, независимо от того, обнажился или не обнажился нижележащий слой.
В случае, когда поток не влечет донных наносов, следует сопоставить глубины местного размыва h1 и (h2 - h d ), где h1 - глубина местного размыва, определяемая для грунта со средним диаметром частиц d1 верхнего слоя по формулам ( 5.4); h2 - то же, но для грунта d2 нижнего слоя; h d - уменьшение глубины местного размыва в нижележащем слое из-за заноса воронки более крупным грунтом верхнего слоя, определяемое по формуле:
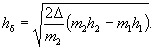 (И.2)
(И.2)
Здесь D - толщина верхнего слоя;
m 1 , m2 - коэффициенты заложения верхового откоса воронок в грунтах со средним диаметром частиц соответственно d1 и d2 (см. таблицу Д.1).
При h1 ³ h2 - h d к расчету следует принимать глубину размыва h = h1.
При h1 < h2 - h d к расчету следует принимать глубину размыва h = h2 - h d .
В формуле ( И.2) при m1h1 ³ m2h2 принимают h d = 0.
И.5 В случае, указанном в п. И.1в, если нижележащий слой состоит из однородного несвязного грунта, то неоднородность вышележащего грунта учитывать не следует. В зависимости от значения средних крупностей частиц рассматриваемых двух грунтов расчет проводят согласно п. И.2 при d1 < d2 или п. И.4 (когда поток не влечет донных наносов) при d1 > d2.
Если нижележащий слой неоднородный со средним диаметром частиц в слое отмостки D, то расчет местного размыва в этом грунте следует проводить по формулам:
а) при e υ ³ υнD и 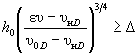 - по формуле ( 5.15)
или ( 5.16);
- по формуле ( 5.15)
или ( 5.16);
б) при e υ ³ υнD , но 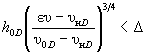 или e υ < υнD по формуле
или e υ < υнD по формуле
h = D +1,7D / p, ( И .3)
где D - толщина верхнего слоя.
При расчете глубин размыва, если имеется движение донных наносов, то они учитываются при определении коэффициента абразивности.
Дальнейший расчет связан с крупностью вышележащего грунта. Если по среднему диаметру частиц вышележащий грунт мельче обнажившегося, то к расчету принимают глубину размыва по формуле ( 5.16) или ( И.3). При этом следует учитывать рекомендации п. 5.3.3.
Если по среднему диаметру частиц вышележащий грунт оказался крупнее обнажившегося, то глубину размыва, полученную по формулам ( 5.15), ( 5.16) или по формуле ( И.3), уменьшают на h d согласно формуле ( И.2), в которой глубину размыва h1 в вышележащем слое определяют по среднему диаметру частиц грунта d1. Вычисленную таким образом глубину размыва h = h2 - h d необходимо сопоставить с глубинами размыва h1 или hн (глубина размыва в наносах, поступающих в воронку при естественной отмостке русла). К расчету принимают глубину размыва, указанную в таблице И.1.
И.6. В случае, указанном в п. И.1г, если верхний слой состоит из связного грунта, то расчет размыва следует производить:
- при обнажении несвязного однородного грунта - согласно п. И.2 с учетом того, что связный грунт не заносит воронку размыва в несвязном материале;
- при обнажении неоднородного несвязного грунта - по формулам ( 5.15) или ( 5.16) или по формуле ( И.3).
Таблица И.1 - Назначение глубины размыва при слоистом залегании грунтов
|
Режим донных наносов |
Дополнительные условия |
Глубина размыва |
Примечание |
|
В верхнем слое однородный грунт |
|||
|
Нет движения наносов |
h 2 - h d ³ h 1 |
h2 - h d |
Глубины размыва h1 и h2 рассчитывают по формулам, рекомендованным п. 4.4 б, независимо от гидравлических |
|
D < h2 - h d < h1 |
h 2 |
||
|
h 2 £ h 1 |
|||
|
h 2 - h d < h1 |
h 1 |
||
|
h 2 > h1 |
|||
|
h 1 > h2 < D |
D |
||
|
Есть движение наносов |
d 1 ³ d 2 |
h 1 |
Глубину размыва h2 рассчитывают по формулам, рекомендованным п. 4.4 б, независимо от гидравлических условий с учетом абразивного воздействия наносов на частицы нижнего слоя |
|
d1 < d2 |
D |
||
|
h 2 £ D |
|||
|
d 1 < d2 |
h 2 |
||
|
h 2 > D , h2 £ h 1 |
|||
|
d 1 < d2 |
h 1 |
||
|
h 2 > D , h2 > h1 |
|||
|
В верхнем слое неоднородный грунт |
|||
|
Нет движения наносов |
Так же, как в однородных грунтах при том же режиме наносов |
Глубину h1 рассчитывают по среднему диаметру частиц грунта верхнего слоя |
|
|
Движение мелких фракций dм |
h 2 - h d ³ hн |
hн |
Глубину размыва h2 рассчитывают по формулам, рекомендованным п. 4.4 б, независимо от гидравлических условий с учетом абразивного воздействия на частицы грунтов нижнего слоя мелких частиц крупностью dм |
|
D < h2 - h d < hн |
h 2 - h d |
||
|
D > h2 - h d < hн |
D |
||
В случае, указанном в п. И.1г, когда нижний слой состоит из связного грунта, расчет размыва следует производить:
- если есть движение наносов, то согласно п. 5.3.3;
- если нет движения наносов, то аналогично случаю И.1б (см. п. И.4) с учетом того, что нижележащий грунт не оказывает абразивного воздействия на связный материал нижнего слоя.
И.7 В случае, указанном в п. И.1д, расчет размыва следует производить для обнаженного слоя применительно к одному из случаев И.1а - И.1г с учетом следующего:
1) вместо
толщины верхнего слоя D принимают суммарную толщину
слоев ![]() , расположенных выше рассматриваемого j-го слоя;
, расположенных выше рассматриваемого j-го слоя;
2) засыпают воронку размыва только несвязные частицы. Воронку местного размыва в обнаженном связном грунте засыпают все вышележащие слои несвязных грунтов, размывающая скорость для которых больше, чем для обнажаемого связного материала (с учетом абразивного воздействия на него несвязных частиц).
Если j-й грунт несвязный, то воронку в нем засыпают более крупные (по среднему диаметру частиц) вышележащие несвязные грунты.
Средний диаметр частиц грунтов вышележащих слоев, которые засыпают воронку размыва, определяют по формуле:
![]() (И.4)
(И.4)
Здесь D i - только те слои несвязного
грунта, в которых di > dj, или при условии ![]() , где υ0cj
- размывающая скорость связного грунта;
, где υ0cj
- размывающая скорость связного грунта;
3) уменьшение глубины местного размыва в j-ом слое из-за заноса воронки более крупным материалом верхних слоев определяют по формуле
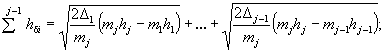 (И.5)
(И.5)
4) вычисленную
глубину размыва в j-м слое h = hj
- ![]() необходимо
сопоставлять с глубинами размыва hн
или hj-1
соответственно в грунте, поступающем в воронку размыва или находящемся в
вышележащем слое, с учетом того, что последний грунт рассматривается как
однородный.
необходимо
сопоставлять с глубинами размыва hн
или hj-1
соответственно в грунте, поступающем в воронку размыва или находящемся в
вышележащем слое, с учетом того, что последний грунт рассматривается как
однородный.
К расчету
принимают глубину размыва, указанную в таблице И.1, в которой принимают h2 = hj, h1
= hj-1, h d = ![]() и D =
и D = ![]() .
.
И.8 Пример. Для условий примера Г.1 (глубина и скорость потока Н = 6,0 м, υ = 1,25 м/с, косина набегания на опору овальной формы в плане шириной b = 4,0 м и длиной L = 12,0 м, a = 15 ° ) определить глубину местного размыва у опоры при следующих геологических условиях:
- после общего размыва на поверхности оказался однородный гравийный материал со средним диаметром частиц 5 мм; толщина слоя 1,0 м;
- ниже - слой глины толщиной 1,6 м с расчетным сцеплением ср = 0,09 × 105 Па;
- под глиной - однородный крупный песок со средним диаметром частиц 0,66 мм.
В воронку размыва в качестве донных наносов поступает песок со средним диаметром частиц 0,46 мм (как в примере Г.1).
Решение . 1. Определим глубину размыва в гравии. Если гидравлическая крупность по графику (см. рисунок А.3) ω = 0,29 м/с, размывающая скорость при глубине потока Н = 6,0 м по рисунку А.1 υ0 = 1,55 м/с, взмучивающая скорость υв = 2,65 м/с.
По формуле ( 5.8)
при ![]() начальная скорость
равна υн = 1,55
начальная скорость
равна υн = 1,55 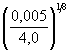 × 0,895 = 0,6 м/с.
× 0,895 = 0,6 м/с.
При коэффициентах формы и косины опоры М = 0,85 и K = 1,22 (см. пример Г.1) по формуле ( И.1) глубина размыва в гравии ( e = 1,115, см. п. 5.2.3)
h =
0,77 × 6,00,4 × 4,00,6 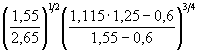 × 0,85 × 1,22 = 2,57 м.
× 0,85 × 1,22 = 2,57 м.
2. Полученная глубина размыва больше гравийного слоя. Следовательно, размыв будет проходить в следующем слое - глине. По аналогии с данными примера Г.4 для глины с таким же расчетным сцеплением имеем:
- размывающую скорость (также принимаем коэффициент шероховатости русла n = 0,028) υ0 = 1,5 м/с;
- толщину отрывающихся отдельностей z = 0,87 мм; их гидравлическую крупность ω = 0,12 м/с и взмучивающую скорость υв = 1,92 м/с. При 3z = 2,61 мм и m = 0,895 (см. выше) по формуле ( 5.8) начальная скорость
υн = 1,5 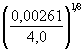 × 0,895 = 0,54 м/с.
× 0,895 = 0,54 м/с.
3. Глубина местного размыва в глине по формуле ( 5.6) при F(b) = 4,00,6 × 0,85 × 1,22 = 2,38 и коэффициенте абразивности e = 1,16 (поскольку по руслу движутся песчаные наносы)
h =
0,77 × 6,00,4 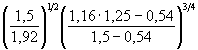 2,38 = 3,2 м.
2,38 = 3,2 м.
4. Гравийный материал будет засыпать воронку, образованную в глине, поскольку (см. п. И.7.2) размывающая скорость гравия υ0 / e = 1,55 / 1,115 = 1,39 м/с больше, чем для глины с учетом абразивного воздействия наносов на эти грунты
![]()
При коэффициентах заложения откоса воронки для гравия m1 = 1,45 и глины m2 = 1,0 (см. таблицу Д.1), толщине слоя гравия D = 1,0 м и соответствующих глубинах местного размыва в глине из-за заноса воронки гравием равно
![]() ,
,
поэтому принимаем h d = 0.
Тогда фактическая глубина размыва в глине h2 - h d = 3,2 м.
Полученная глубина размыва больше суммарной толщины слоев гравия и глины 1,0 + 1,6 = 2,6 м, поэтому вскрывается нижележащий грунт - песок, в котором будет происходить размыв.
5. Для песка со средним диаметром частиц 0,66 мм имеем (по аналогии, как для гравия): ω = 0,08 м/с; υ0 = 0,92 м/с; υв = 1,67 м/с и υн = 0,28 м/с.
По формуле ( 5.2) глубина размыва в песке
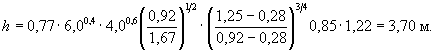
6. Полученная глубина размыва больше толщины слоев над вскрываемым грунтом (песком), поэтому указанный грунт будет участвовать в процессе местного размыва. В то же время вышележащие слои (включая сюда и донные наносы) могут оказывать влияние на формирование глубины размыва:
- во-первых, более крупный (гравийный) грунт верхнего слоя будет уменьшать глубину размыва в песке (гравий будет ссыпаться в воронку размыва);
- во-вторых, поступающие в воронку размыва наносы также могут уменьшить глубину размыва.
7. Занос воронки будет происходить только гравийным материалом (отрываемые отдельности глины будут уноситься потоком). При коэффициентах заложения откосов воронки для гравия m1 = 1,45 и нижележащего слоя песка m2 = 1,6 (см. таблицу Д.1), толщине слоя гравия D = 1,0 м и соответствующих глубинах местного размыва h1 = 2,57 м и h2 = 3,7 м по формуле ( И.2) уменьшение глубины местного размыва в песке из-за заноса воронки гравием равно
![]()
Соответственно h2 - h d = 3,7 - 1,65 = 2,05 м.
8. Полученная глубина размыва в песке с учетом заноса гравием оказалась меньше и глубины размыва в заносимом материале (2,57 м), и суммарной толщины слоев гравия и глины (2,60 м). Поэтому, если бы поток не влек донные наносы, к расчету следовало бы принимать глубину размыва до отметки верха песка (2,60 м).
Так как поток влечет наносы, то следует сопоставить полученную глубину размыва 2,60 м с глубиной, которую формируют донные наносы. Из примера Г.1 известно, что эта глубина размыва равна 3,4 м, что больше полученной. Следовательно, окончательно расчетная глубина местного размыва в рассматриваемых условиях равна 2,60 м.
9. Следует обратить внимание на казалось бы парадоксальное обстоятельство: если бы не было слоя глины, глубина размыва (принципиально) оказалась бы меньше принятой, т.е. h = 2,57 м. Эту глубину следует назначать согласно таблице И.1 (при дополнительных условиях h2 - h d < h1 и h2 > h1).
Такой «парадокс» объясняется тем, что при вскрыше нижнего песчаного слоя размеры воронки в плане значительно превосходят эти размеры при формировании воронки в связном материале (коэффициент заложения откосов воронки в глине и песке соответственно равны 1,0 и 1,6). Поэтому и больший объем гравия в первом случае будет засыпать воронку.
Приложение К
(рекомендуемое)
ЗНАЧЕНИЕ КОЭФФИЦИЕНТА Kt ПРИ ОПРЕДЕЛЕНИИ РАЗМЫВОВ У ДАМБ И КОНУСОВ МОСТА
Коэффициент Kt, характеризующий увеличение скорости потока в голове дамбы или в верховой части конуса при длине сооружения вверх по течению от оси подходной насыпи lвф меньше требуемой длины (вылета) lв для плавного его обтекания, следует определять по таблице К.1, составленной по формуле
K t = ехр[0,35 l 2 (1 - lвф / lв)2],
где l - требуемое для плавного обтекания отношение полуосей дамбы.
Расчетные плановые размеры дамб и конусов рекомендуется определять в плоскости, соответствующей РУВВ - расчетному уровню воды в створе моста.
Если при расчете
коэффициента K t окажется, что Kt
³ 0,75 ![]() , то следует принимать Kt
= 0,75
, то следует принимать Kt
= 0,75 ![]() ,
где υдм - расчетная скорость потока у подошвы в створе моста (в
процессе общего размыва на момент наибольшего подпора).
,
где υдм - расчетная скорость потока у подошвы в створе моста (в
процессе общего размыва на момент наибольшего подпора).
Таблица К.1 - Коэффициент K t
|
lвф lв |
Значение Kt при требуемом l |
||||
|
1,25 |
1,6 |
1,75 |
2,0 |
2,25 |
|
|
0,9 |
1,00 |
1,00 |
1,01 |
1,01 |
1,02 |
|
0,8 |
1,02 |
1,03 |
1,04 |
1,06 |
1,09 |
|
0,7 |
1,05 |
1,07 |
1,10 |
1,13 |
1,22 |
|
0,6 |
1,09 |
1,13 |
1,19 |
1,25 |
1,42 |
|
0,5 |
1,15 |
1,22 |
1,30 |
1,42 |
1,72 |
|
0,4 |
1,22 |
1,33 |
1,47 |
1,66 |
2,21 |
|
0,3 |
1,30 |
1,47 |
1,69 |
1,98 |
2,91 |
|
0,2 |
1,42 |
1,60 |
1,98 |
2,44 |
4,04 |
|
0,1 |
1,55 |
1,89 |
2,12 |
3,10 |
5,90 |
Приложение Л
(справочное)
ПРИМЕР РАСЧЕТА ГЛУБИН МЕСТНОГО РАЗМЫВА У СТРУЕНАПРАВЛЯЮЩЕЙ ДАМБЫ И КОНУСА МОСТА
Пример. Определить глубину местного размыва у левобережной струенаправляющей дамбы и правобережного конуса. В расчетный паводок коэффициенты стеснения потока подходами на левой пойме d л = 0,42, на правой d п = 0,06; глубина воды у голов дамб в бытовых условиях соответственно Нбл = 2,0 м и Нбп = 2,5 м; средний уклон свободной поверхности потока в районе моста i = 0,0002.
Левая пойма сложена суглинком с расчетным сцеплением ср = 2,02 × 105 Па; правая пойма - мелким однородным песком со средним диаметром частиц 0,3 мм.
В процессе проектирования мостового перехода определены предмостовой подпор D h в = 0,25 м и расстояние Х0 = 650 м от моста до вертикали, где устанавливается предмостовой подпор.
Плановые размеры левобережной дамбы приняты полученными по расчету (т.е. дамба имеет достаточную длину вылета и хорошо обтекается потоком); крутизна откосов дамбы m = 2.
У правого устоя запроектирован конус (учитывая малое стеснение потока на пойме). Ширина его вверх по течению от оси подходной насыпи на уровне УВВ составляет lвф = 25 м, хотя по расчету требуется дамба с длиной вылета lв = 42,5 м и отношением полуосей l = 1,5. Крутизна откосов конуса m = 1,5.
Решение . 1. Левая пойма пропускает значительно больший расход воды, чем правая, поэтому с нее надо начинать расчет размывов у дамб. Для этого, в первую очередь, определим глубину Нгл = Нгм и скорость υгл = υгм потока у подошвы головы левобережной дамбы.
2. Глубину потока у подошвы головы левобережной дамбы определим по формуле ( 6.10)
Н гм = 2,0 + 0,25 = 2,25 м.
По формуле ( 6.5) коэффициент Шези (принимаем коэффициент шероховатости русла nр = 0,03)
С гм = 2,251/6/0,03 = 38,3 (м0,5/с).
3. С учетом относительного расхода воды, проходящего на ширине отверстия моста при отсутствии стеснения,
QL / Q = 1 - ( d л + d п ) = 1 - (0,42 + 0,06) = 0,52 и соответственно
Q / Q L = 1 / 0,52 = 1,925 по формуле ( 6.9)
![]()
4. По формуле ( 6.8) средний уклон свободной поверхности потока перед мостом, как бы вызванный стеснением левой мощной поймы,
i м(м) = 0,0002 + 0,845 × 0,25 / 650 = 0,0002 + 0,000325 = 0,525 × 10-3.
5. По формуле ( 6.3) скорость потока в голове левобережной дамбы
υг(м) = 38,3 ![]() (0,2 × 10-6 × 0,525)1/4 = 0,68
м/с.
(0,2 × 10-6 × 0,525)1/4 = 0,68
м/с.
6. Для правобережного конуса по формуле ( 6.10)
Н гп = Нгс = 2,5 + 0,25 = 2,75 м.
7. Для определения скорости потока в верховой части правобережного конуса υr(с) по формуле ( 6.4) предварительно найдем:
- по формуле ( 6.9)
![]()
- по формуле ( 6.8)
i м(с) = 0,0002 + 0,092 × 0,25 / 650 = 0,235 × 10 - 3 ;
- по формуле ( 6.6)
b = 1,55 × 0,68 / ![]() = 0,224 > 0,2.
= 0,224 > 0,2.
Подставляя вычисленные значения в формулу ( 6.4), получим
υг(с) = 0,68 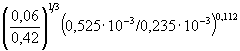 = 0,36 м/с.
= 0,36 м/с.
8. Глубину размыва в голове левобережной дамбы определим по формуле ( 6.1) с учетом того, что ее длина вылета достаточная и она хорошо обтекается потоком ( K l = K l = 1). Для суглинка с расчетным сцеплением Ср = 0,02 × 105 Па, коэффициенте шероховатости русла nр = 0,03 и глубине потока 2,25 м по графику (см. рисунок А.2) размывающая скорость υ0 = 0,62 м/с. При коэффициенте заложения откоса дамбы m = 2 K m = 0,77 (см. п. 6.1.1). Тогда:
![]()
9. Расчет глубины размыва в верховой части правого конуса следует также выполнять по формуле ( 6.1) с учетом того, что его ширина вверх по течению от оси подходной насыпи составляет lвф = 25 м, тогда как для плавного обтекания требуется lв = 42,5 м. При этом следует, что такой конус будет плохо (т.е. с отрывными течениями и водоворотными зонами) обтекаться потоком и поэтому K l = 0,85. Из-за недостаточных плановых размеров конуса по таблице К.1 при lвф / lв = 25,0 / 42,5 = 0,59 и требуемом отношении полуосей сооружения l = 1,5 получаем K l = 1,14. При m = 1,5 K m = 0,8 (см. п. 6.1.1).
Для мелкого однородного песка со средним диаметром частиц 0,3 мм при глубине потока Нгс = 2,75 м неразмывающая скорость по графику (см. рисунок А.1) υ0 = 0,6 м/с. Тогда
![]()
Приложение М
(обязательное)
РАСЧЕТНАЯ ШИРИНА b БЕРЕГОВЫХ ОПОР И ПОПЕРЕЧНЫХ РЕГУЛЯЦИОННЫХ СООРУЖЕНИЙ
За расчетную ширину b береговых опор следует принимать среднюю ширину под водой (до местного размыва) боковой грани опоры, перпендикулярной направлению потока и выступающей из конуса (рисунок М.1).
За расчетную ширину b поперечного регуляционного сооружения следует принимать проекцию его длины l0 на нормаль к насыпи или берегу (рисунок М.2) и определять по формуле
b = l0sin a , ( М .1)
где a - угол примыкания поперечного сооружения к насыпи или берегу.
Угол a должен отсчитываться от продольной оси сооружения вниз по течению; на криволинейном участке - между осью сооружения и касательной к оси насыпи или линии берега в точке примыкания к ним. Длину поперечного сооружения l0, равную средней длине его продольного сечения под водой, следует определять по формуле
l 0 = lниз - 0,5mН. (М.2)
где lниз - длина поперечного сооружения понизу вдоль его продольной оси.
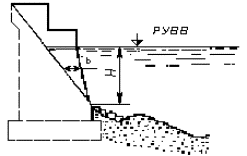
Рисунок М.1 - Расчетная ширина береговой опоры
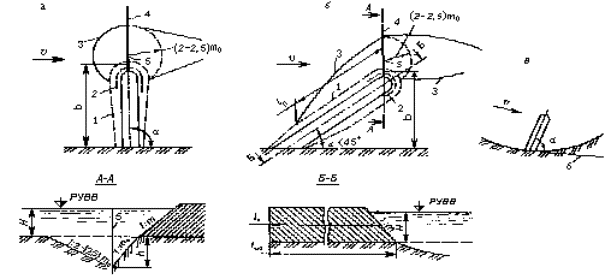
Рисунок М.2 - План поперечных сооружений:
а - при угле примыкания поперечного сооружения a ³ 45 °; б - то же, при a < 45 °; в - определение угла примыкания на криволинейном участке; 1 - подошва (до размыва) откоса сооружения; 2 - урез воды; 3 - схематизированный контур воронки размыва; 4 - расчетный створ; 5 - вертикаль с наибольшей глубиной размыва; 6 - касательная к линии берега
Приложение Н
(рекомендуемое)
ЗНАЧЕНИЯ КОЭФФИЦИЕНТА K υ ПРИ ОПРЕДЕЛЕНИИ РАЗМЫВОВ У ПОПЕРЕЧНЫХ СЕЧЕНИЙ
Коэффициент K υ , характеризующий поступление наносов в воронку размыва, следует принимать равным:
- при расположении поперечного сооружения на пойме, размывах в связных грунтах или при υ £ υ0 Kυ = 1;
- при ³ 1,35υ0 и расположении поперечного сооружения в русле
K υ = Kυmax = 0,96(H / d)0,05; ( Н .1)
- при υ0 < υ < 1,35υ0 и расположении поперечного сооружения в русле
![]() (Н.2)
(Н.2)
Для ускорения определения коэффициента K υmax по формуле ( 1) рекомендуется пользоваться следующими данными:
Н / d 50 100 200 400 600
K υmax 2,17 1,21 1,25 1,30 1,31
Н / d 1000 2000 40000 6000 10000
K υmax 1,35 1,41 1,45 1,48 1,52
Приложение П
(справочное)
ПРИМЕРЫ РАСЧЕТА РАЗМЫВОВ У ПОПЕРЕЧНЫХ СООРУЖЕНИЙ И БЕРЕГОВЫХ ОПОР
Пример П. 1. Определить глубину местного размыва у шпоры, отжимающей поток на криволинейном русле от насыпи, подошва которой попадает в русло. Русло сложено однородным песком со средним диаметром частиц 0,5 мм; у подошвы насыпи глубина и скорость потока соответственно равны Н = 6,5 м и υ = 1,0 м/с.
Шпора запроектирована длиной понизу lниз = 25 м с откосом m = 2; угол примыкания к насыпи a = 35 ° (см. рисунок М.2).
Решение . 1. Вначале согласно приложению М определим расчетную ширину шпоры b. По формуле ( М.2) длина шпоры
l 0 = 25 - 0,5 × 2 × 6,5 = 18,0 м,
а по формуле ( М.1)
b = 18,0sin 35 ° = 10,3 м .
2. Глубину местного размыва будем определять по формуле ( 7.1), поскольку b / Н > 1.
Предварительно в этой формуле определим:
- по формуле ( 7.4) скорость потока в голове шпоры
υг = 1,0 + 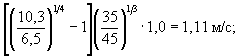
- по рисунку А.1 размывающая скорость при d = 0,5 мм и Н = 6,5 м, υ0 = 0,87 м/с;
- по формуле ( Н.2)
при υ0 < υ < 1,35υ0 и K υmax = 0,96 (Н
/ d)0,05 = 0,96 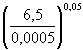 = 1,55.
= 1,55.
K υ = 1 + (1,55 - 1) × (1,0 - 0,87) / (0,35 × 0,87) = 1,235;
- при m = 2 согласно п. 6.1.1 K m = 0,77, тогда
h =
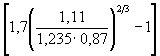 6,5 × 0,77 = 3,67 м.
6,5 × 0,77 = 3,67 м.
Пример П.2. Для условий примера П.1 определить глубину местного размыва у такой же шпоры, но устраиваемой для отжима потока от вогнутого берега вровень с берегом. При проходе воды в бровках русла глубина и скорость потока у берега Нбр = 4,0 м и υбр = 0,8 м/с (высота сооружения Н1 = Нбр = 4,0 м).
Решение . 1. Уточним расчетную ширину шпоры l0 по формуле ( М.2)
l 0 = 25 - 0,5 × 2 × 4 = 21 м;
по формуле ( М.1) b = 21sin 35 ° = 12,05 м.
2. Для условий прохода расчетного паводка (Н = 6,5 м, υ = 1,0 м/с) требуется уточнение скорости потока в голове шпоры υг и весового коэффициента f1, учитывающего снижение глубины местного размыва за счет затопления сооружения.
По формуле ( 7.4)
υг = 1,0 + 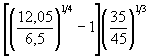 1,0
= 1,15 м/с.
1,0
= 1,15 м/с.
По формуле ( 5.11)
(при ![]() = 0,615 > 0,3) A = 1 и j = 1/3 f1 =
= 0,615 > 0,3) A = 1 и j = 1/3 f1 = 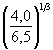 = 0,85.
= 0,85.
3. Для условий прохода расчетного паводка по формуле ( 7.1) с учетом коэффициента f1 (см. п. 7.6) глубина местного размыва равна
h =
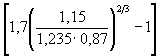 6,5 × 0,77 × 0,85 = 3,36 м.
6,5 × 0,77 × 0,85 = 3,36 м.
4. Согласно п. 7.6 необходимо определить глубину размыва при проходе потока в бровках русла.
По аналогии с проводимыми действиями в примере П.1 имеем:
υг = 0,8 + 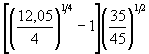 0,8 = 1,03 м/с;
0,8 = 1,03 м/с;
K υmax = 0,96 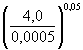 = 1,5; υ0
= 0,77 м/с, υ0 < υ < 1,35υ0;
= 1,5; υ0
= 0,77 м/с, υ0 < υ < 1,35υ0;
K υ = 1 + (1,5 - 1)(0,88 - 0,77) / (0,35 × 0,77) = 1,20.
Тогда по формуле ( 7.1)
h =
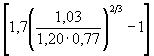 4 × 0,77 = 2,6 м.
4 × 0,77 = 2,6 м.
5. К расчету следует принимать большую из полученных глубин местного размыва, т.е. 3,36 м.
Пример П.3. Для условий, приведенных в примере П.1 (Н = 6,5 м, υ = 1,0 м/с, d = 0,5 мм) определить глубину местного размыва у береговой опоры (устоя), боковые грани которой не обсыпаны конусом. Причем боковая грань, перпендикулярная направлению потока, в плоскости расчетного уровня (УВВ) выступает из конуса на bmax = 10 м (см. рисунок М.1).
Решение . 1. Согласно приложению М расчетная ширина опоры равна средней ширине под водой боковой ее грани, т.е.
b = bmax / 2 = 5 м .
2. Поскольку b / Н < 1, то глубину местного размыва следует определять по формуле ( 7.2), в которой известно из примера П.1 Kυ = 1,235 и υ0 = 0,87 м/с.
Согласно п. 6.1.1 для вертикальной стенки (m = 0) K m = 1.
По формуле ( 7.3) с учетом b / Н < 1 скорость потока у боковой грани опоры υг = υ = 1,0 м/с.
Тогда h = 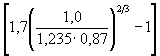 5 × 1 = 3,07 м.
5 × 1 = 3,07 м.
Приложение Р
(справочное)
ПРИМЕРЫ РАСЧЕТА РАЗМЫВОВ У ПОДОШВЫ НАСЫПИ НА ПРИЖИМНОМ УЧАСТКЕ РЕКИ ОТ ПРОДОЛЬНЫХ ТЕЧЕНИЙ ПРИ ОТСУТСТВИИ И НАЛИЧИИ ВОЛНОВЫХ ВОЗДЕЙСТВИЙ
Пример Р.1. Определить глубину размыва у подошвы насыпи с откосом, попавшим в русло, в расчетный паводок. Глубина и скорость потока соответственно равны Н = 6,5 м и υ = 1,4 м/с. Русло сложено суглинком с расчетным сцеплением ср = 0,07 × 105 Па; поток в русле влечет донные наносы со средним диаметром частиц d = 0,3 мм. Коэффициент шероховатости русла nр = 0,03.
Решение . По формуле ( 8.6) глубина размыва
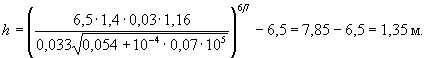
Согласно п. 8.2б, следует проверить по формуле ( 8.8) возможность заноса полученной глубины размыва донными наносами
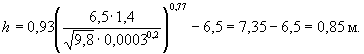
К расчету следует принять глубину размыва h = 0,85 м.
Пример Р.2. Для условий примера Р.1 определить глубину размыва у подошвы насыпи от продольных течений при наличии волновых воздействий (расчетная высота волны 0,5 м; средний период волн Т = 1,7 с).
Решение . Вначале определим коэффициент x , учитывающий увеличение размыва от продольных течений при наличии волновых воздействий. При плотности частиц грунта r = 2650 кг/м3 (и воды r 0 = 1000 кг/м3) по формуле ( 8.10)
![]()
По формуле ( 8.9)
![]()
Подставляя коэффициент x в формулу ( 8.8), имеем глубину размыва
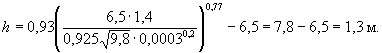
Примечание. Расчет проведен по формуле ( 8.8), а не ( 8.6), поскольку из примера Р.1 выяснено, что глубина размыва у подошвы насыпи определяется динамическим равновесием наносов на этом участке русла.
Приложение С
(рекомендуемое)
ОПРЕДЕЛЕНИЕ ГЛУБИНЫ РАЗМЫВА У ПОДОШВЫ НАСЫПИ ОТ ВОЛНОВЫХ ВОЗДЕЙСТВИЙ
С.1 При обрушении волны на откос она разделяется на два противоположных по направлению потока (рисунок С.1). Из потока, идущего вверх по откосу, формируется так называемый накат волны; нисходящие струи, достигая неукрепленной подошвы откоса, могут вызвать размыв дна у основания откосного сооружения (насыпи).
С.2 Скорость струй, идущих вниз по откосу, убывает с глубиной потока. Максимальную скорость нисходящего потока у подошвы откоса (или максимальную донную скорость υдmax) рекомендуется определять по формуле
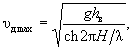 (С.1)
(С.1)
где hв - расчетная высота волны;
l - средняя длина волны;
Н - глубина воды у подошвы насыпи, исчисляемая от статистического подпертого уровня воды перед насыпью (ПУВВ), складывается из глубины воды у насыпи до размыва Нб и глубины размыва h.
Для определения
значения гиперболического косинуса ![]() можно пользоваться
графиком (рисунок С.2).
можно пользоваться
графиком (рисунок С.2).
Формула ( С.1) справедлива при коэффициенте заложения откоса m £ 3. При более пологих откосах формула завышает значение максимальной донной скорости.
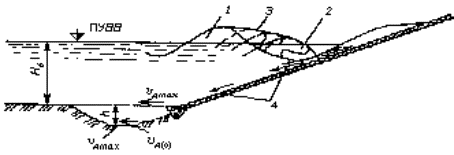
Рисунок С.1 - Схема разрушения волны и формирования воронки размыва:
1 - гребень волны до разрушения; 2 - опрокинутый гребень в момент обрушения волны на откос; 3 - траектория движения частиц воды на гребне волны; 4 - исходящие струи, образующиеся при разрушении волны
С.3 Если окажется, что максимальная донная скорость меньше размывающей донной скорости υд(0) для грунтов в основании насыпи, то размыва у подошвы насыпи не будет.
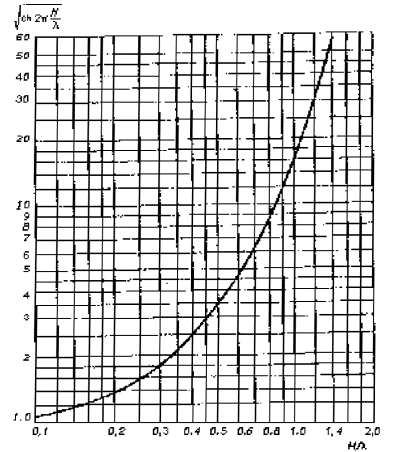
Рисунок
С.2 - Значения гиперболической функции ![]()
При υдmax > υд(0) следует задаться глубиной размыва h, определить максимальную донную скорость υдmax при глубине потока перед насыпью Н = Нб + h и сопоставить с υд(0). Операция повторяется до получения υдmax £ υд(0).
С.4 По полученной глубине размыва h задают необходимый объем рисбермы для защиты подошвы насыпи от подмыва. При этом крупность камня в рисберме должна обеспечивать устойчивость от воздействия исходящего с откоса потока при глубине воды у насыпи Н. Для предотвращения размывов у подошвы откосов основание насыпи следует укреплять на ширину не менее глубины воды перед откосом.
Пример. Определить возможный размыв и соответственно необходимость укрепления подошвы откоса от волнового воздействия при глубине потока перед насыпью Н = 3,2 м, расчетной высоте и средней длине волны соответственно hв = 0,75 м l = 8,4 м; в основании насыпи - суглинок с расчетным сцеплением ср = 0,04 × 105 Па.
Решение . По формуле ( С.1) определяем максимальную
донную скорость у подошвы откоса. При ![]() по графику (см.
рисунок С.2)
имеем
по графику (см.
рисунок С.2)
имеем ![]() . Тогда
. Тогда ![]()
2. По формуле ( 8.12) эквивалентный диаметр суглинка dэ = 7,5(0,1 + 10 × 0,04) = 3,08 мм, для которого размывающая донная скорость по графику (см. рисунок 8.1) υд(0) = 0,52 м/с.
Поскольку υдmax > υд(0), необходимо укрепление подошвы откоса.
3. По графику (см. рисунок 8.1) из условия υд(0) ³ υдmax крупность камня dк, которым можно укреплять подошву откоса, равна dк ³ 20 мм.
4. Для определения размыва у подошвы насыпи без его укрепления поступим следующим образом:
- из формулы ( С.1) определяем требуемое значение гиперболической функции при υдmax = υд(0) = 0,52 м/с
![]()
- по графику (см. рисунок С.2) находим для полученного значения гиперболической функции H / l = 0,63;
- определяем глубину потока у подошвы насыпи после размыва Н = 0,63 × 8,4 = 5,28 м; откуда глубина размыва h = 5,28 - 3,2 = 2,08 м.
Приложение Т
(рекомендуемое)
ОПРЕДЕЛЕНИЕ РАДИУСОВ КРИВИЗНЫ ИЗЛУЧИНЫ
Т.1 Радиус кривизны потока у вогнутого берега или прислоненного откоса насыпи определяют по формуле
r = rи + Вр / 2, (Т.1)
где rи - минимальный радиус кривизны излучины по оси русла шириной Вр.
Т.2 Радиус кривизны потока по оси русла rи, когда поток не выходит из бровок русла, совпадает с радиусом кривизны излучины и может быть определен по формуле
r и = rи(бр) = ![]() (Т.2)
(Т.2)
где аи - расстояние от середины шага излучины l и до ее вершины по оси русла (рисунок Т.1).
Т.3 При выходе воды на пойму радиус кривизны потока rи увеличивается по сравнению с тем же в бровках русла rи(бр) и равен
r и = rи(бр) 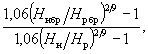 (Т.3)
(Т.3)
где Нр, Нн - средняя глубина потока и глубина потока у вогнутого берега в рассматриваемом створе русла при проходе расчетного паводка;
Н рбр , Нибр - соответствующие глубины потока в бровках русла.
При устройстве срезки грунта со стороны выпуклого (противоположного укрепляемому) берега радиус кривизны потока rи при выходе на пойму можно принимать по формуле ( Т.3) с коэффициентом 1,1 - 1,2.
Т.4 Если между продольной осью насыпи и берегом на входе трассы в русло будет угол более 10 ° , то для входного участка, составляющего не менее ширины нестесненного русла Вр, радиус кривизны русла rи независимо от уровня воды рекомендуется принимать по формуле ( Т.2).
Пример. Определить глубину местного размыва у подошвы насыпи (см. рисунок Т.1), возникшего в связи с нарушением естественного хода руслового процесса.
Русло шириной Вр = 260 м сложено однородным песком со средним диаметром частиц 0,5 мм; минимальный радиус кривизны излучины по оси русла rи = 600 м. Когда поток достигает бровки русла, средняя глубина в русле Нрбр = 4 м; глубина у вогнутого берега Нибр = 6 м; средняя скорость потока υрбр = 0,8 м/с. При расчетном паводке средние глубина и скорость потока в русле Нр = 6,5 м и υр = 1,0 м/с. Речной откос насыпи крутизной m = 2 укреплен каменной наброской.
Решение . 1. Вначале определим радиус кривизны потока по оси русла rи при выходе воды на пойму. При средней глубине потока в русле при расчетном уровне и уровне в бровках русла Нр = 6,5 м и Нрбр = 4 м, а также глубине потока у вогнутого берега (у подошвы насыпи) при расчетном уровне
Н и = Нибр + (Нр - Нрбр) = 6 + (6,5 - 4) = 8,5 м
по формуле ( Т.3)
![]()
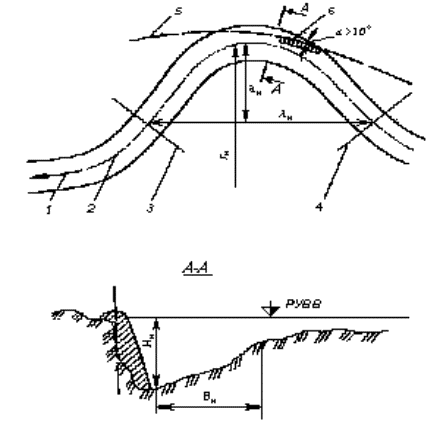
Рисунок Т.1 - К определению радиуса кривизны потока rи:
1 - направление течения; 2 - ось русла; 3 - конец и начало излучины; 5, 6 - трасса и ее входной участок
2. Радиус кривизны потока у вогнутого берега по формуле ( Т.1)
r = 680 + 260 / 2 = 810 м.
3. По графику (см. рисунок А.1) размывающая скорость для частиц грунта 0,5 мм и глубине потока Н = Нр = 6,5 м υ0 = 0,87 м/с.
4. Определяем для расчетного уровня (при проходе расчетного паводка) глубину местного размыва у подошвы насыпи по формуле ( 8.13) при коэффициенте шероховатости укрепления (каменной наброски) n = 0,03 и коэффициенте формы укрепления М = 1 [см. пояснения к формуле ( 8.13)].
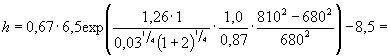
= 0,67 × 6,5 × e1,12 - 8,5 = 13,3 - 8,5 = 4,8 м.
5. Согласно п. 8.8 необходимо также определить глубину местного размыва у подошвы насыпи, когда поток только достиг бровки берега.
По формуле ( 8.13)
при Н = Нрбр = 4 м, υр = υрбр =
0,8 м/с, υ0 = 0,77 м/с (при глубине потока 4 м), rи = 600 м и r = 600 + ![]() = 730 м глубина
размыва равна
= 730 м глубина
размыва равна
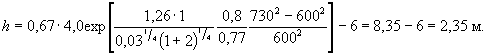
6. Поскольку полученная глубина размыва меньше рассчитанной при расчетном уровне, за искомую следует принимать h = 4,8 м.
7. Для уменьшения глубины размыва устроим срезку грунта со стороны выпуклого берега. Тогда радиус кривизны потока в русле при расчетном уровне примем равным 1,15 × rи = 1,15 × 680 » 780 м (см. п. Т.3), r = 780 + 260 / 2 = 910 м, и глубина размыва по формуле ( Т.3) будет равна 2,85 м.
Как видим, устройство срезки грунта на противоположном (укрепляемому) берегу является эффективным методом снижения размывов у вогнутых берегов русел.
Ключевые слова: глубина местного размыва, опора моста, струенаправляющая дамба, конус моста, подошва насыпи, регуляционные сооружения, грунты связные и несвязные.
СОДЕРЖАНИЕ
|
1 Область применения . 2 2 Нормативные ссылки . 2 3 Определения . 2 4 Общие положения . 2 5 Промежуточные опоры мостов . 3 5.1 Размыв в однородных несвязных грунтах . 3 5.2 Учет неоднородности несвязных грунтов . 9 5.3 Размыв в связных грунтах . 11 5.4 Учет слоистого залегания грунтов . 12 6 Струенаправляющие дамбы и конуса мостов . 13 6.1 Размыв в однородных несвязных и связных грунтах . 13 6.2 Учет неоднородности и слоистого залегания грунтов . 14 7 Поперечные регуляционные сооружения и береговые опоры .. 16 8 Размыв у подошв насыпей и закрепленных берегов русел от продольных течений, волновых воздействий и нарушения естественного хода руслового процесса . 18 Приложение А. Расчетные характеристики наносов и грунтов . 21 Приложение Б. Коэффициент формы свайных фундаментов . 27 Приложение В. Значения приведенной ширины b a характерных форм опор . 29 Приложение Г. Примеры расчета местного размыва у промежуточных опор мостов . 30 Приложение Д. Уменьшение глубины размыва dт за счет ступеней на границе элементов промежуточной опоры, находящихся выше отметки общего размыва . 34 Приложение Е. Уменьшение глубины размыва dф за счет обнажаемой в процессе местного размыва части массивного фундамента . 37 Приложение Ж. Определение среднего диаметра частиц слоя отмостки и их содержание в грунте при расчете местных размывов у опор . 38 Приложение И. Расчет размывов у промежуточных опор при слоистом залегании грунтов . 41 Приложение К. Значение коэффициента kt при определении размывов у дамб и конусов моста . 46 Приложение Л. Пример расчета глубин местного размыва у струенаправляющей дамбы и конуса моста . 47 Приложение М. Расчетная ширина b береговых опор и поперечных регуляционных сооружений . 48 Приложение Н. Значения коэффициента k υ при определении размывов у поперечных сечений . 49 Приложение П. Примеры расчета размывов у поперечных сооружений и береговых опор . 50 Приложение Р. Примеры расчета размывов у подошвы насыпи на прижимном участке реки от продольных течений при отсутствии и наличии волновых воздействий . 52 Приложение С. Определение глубины размыва у подошвы насыпи от волновых воздействий . 53 Приложение Т. Определение радиусов кривизны излучины .. 55 |